Resource	Info
Paper	https://arxiv.org/abs/2501.12570
Code & Data	https://github.com/StarDewXXX/O1-Pruner
Public	arXiv
Date	2025.03.18

Summary Overview

本文针对于当前 Reasoning LLM 出现的 Long-CoT 问题进行改进，提出来 Length Harmonizing Fine-Tuning (O1-Pruner) 的方法，使用 RL 的方法微调模型，使其输出的 CoT 长度降低。同时文章中还注意到一个现象，并非是越长的 CoT 能获得越好的效果。

Main Content

我们观察到，漫长的推理LLM中的推理过程经常表现出重要的裁员，从而导致计算资源的使用效率低下。我们的方法引入了 Length-Harmonizing Reward，该奖励明确地奖励了更短的解决方案，同时惩罚准确性退化。

A Simple Experiment:

我们从 MATH 测试集中随机选择了64个问题（对于QWQ-32B，我们首先过滤了 hard samples）。对于每个问题，我们使用 MARCO-O1 和 QWQ-32B 生成了512个解决方案。对于每个问题，我们将所有候选解决方案分为4个间隔，并随后计算每个间隔的准确率。

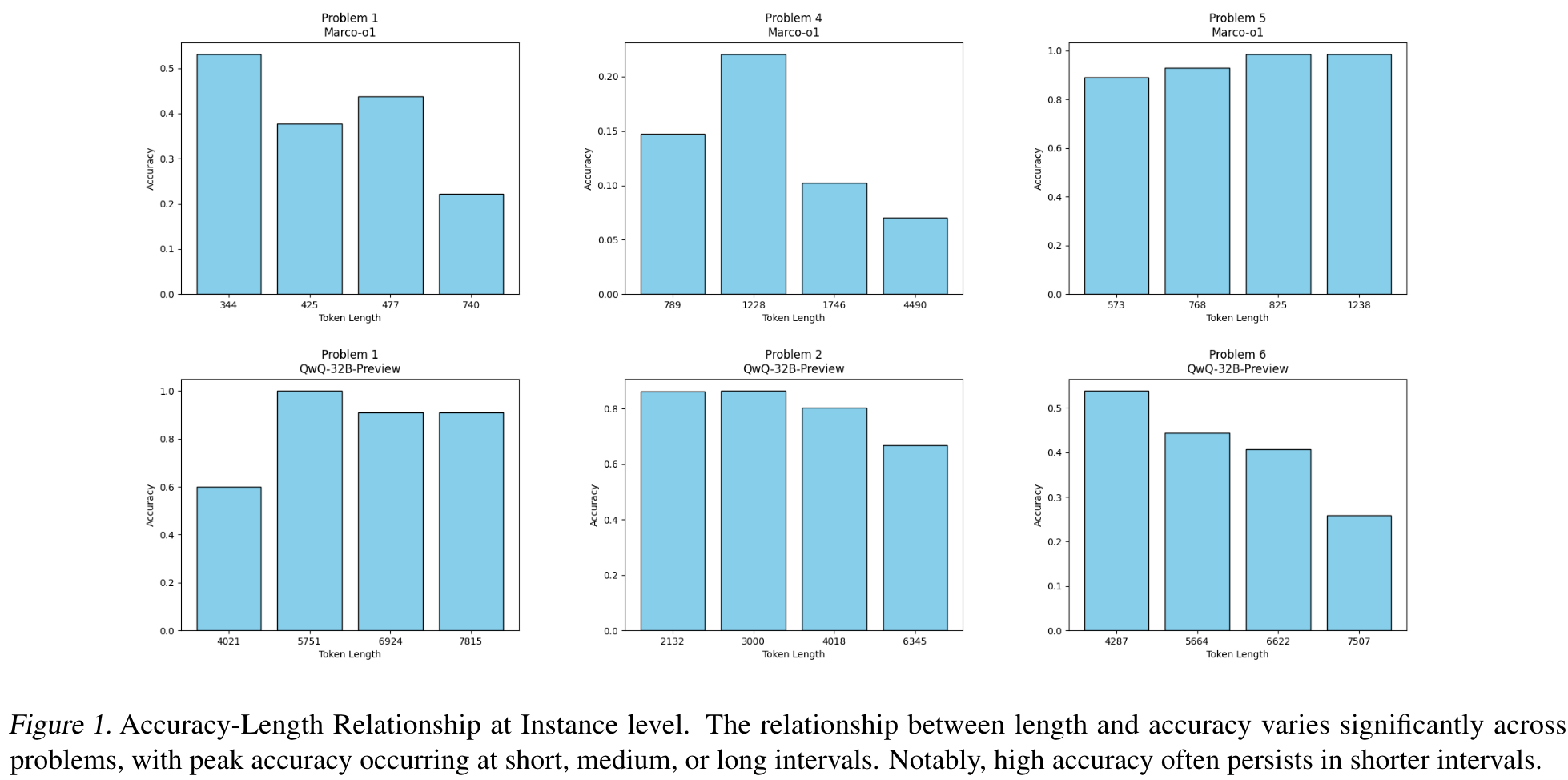
因此，我们可以得出结论，在推理过程中，长期思考模型表现出长度不和谐的现象，这在推理阶段导致了冗余的计算开销。这种推理的冗余性可以得到缓解，因为即使在较短的长度下仍保持高精度。

Length-Harmonizing Fine-Tuning (O1-Pruner)

To address this, we propose an optimizatoin objective that ensures no degradation in accuracy while tackling the issue from two perspectives. First, at the overall level, we aim to shorten the reasoning paths. Second, we encourage the model to output shorter answers for simpler problems, while for more complex problems, we guide the model to learn the correct reasoning paths, which, according to the inference scaling law, typically involve longer reasoning sequences.

We subtract a constant 1 from the optimization objective to ensure that the initial expected value of the optimization is zero.

Constraint condition:

Therefore, we can establish our optimization objective as:

To solve this constrained optimization problem, we incorporate constraint into the objective function as a penalty term. Specifically, the constraint on accuracy is added to the objective with a penalty weight $\lambda\geq0:$

By reorganizing the terms related with reference model $\pi_{ref}$, we have:

In practice, we approximate the expection terms related with $\pi_{ref}$ by sampling. For each $x$, we sample for $K$ times from $\pi_{ref}(\cdot|x)$ and calculate the mean value:

This approach is widely employed in Policy Gradient with Baseline. Furthermore, a recently proposed method GRPO adopts a similar technique to reduce training overhead. Based on this technique, our objective can be approximated as:

Defining the Length-Harmonizing Reward $R_{LH}(x, y) = \frac{\bar{L}_\text{ref}(x)}{L(y)} - 1 + \lambda \big(A(x, y) - \bar{A}_\text{ref}(x)\big)$, the loss function of off-policy-version Length-Harmonizing Fine-Tuning is

Evaluation Metric

• Accuracy

• Length

• AES: Accuracy-Efficiency Score (AES).

  $\Delta\text{Length}=\frac{\text{Length}_{\text{baseline}}-\text{Length}_{\text{baseline}}}{\text{Length}_{\text{baseline}}}$

  $\Delta\text{Acc}=\frac{\text{Acc}_{\text{model}}-\text{Acc}_\text{baseline}}{\text{Acc}_{\text{baseline}}}$

$\text{AES} = \begin{cases} \alpha \cdot \Delta \text{Length} + \beta \cdot |\Delta \text{Acc}|, & \text{if } \Delta \text{Acc} \geq 0, \\ \alpha \cdot \Delta \text{Length} - \gamma \cdot |\Delta \text{Acc}|, & \text{if } \Delta \text{Acc} < 0. \end{cases}$

Main Result

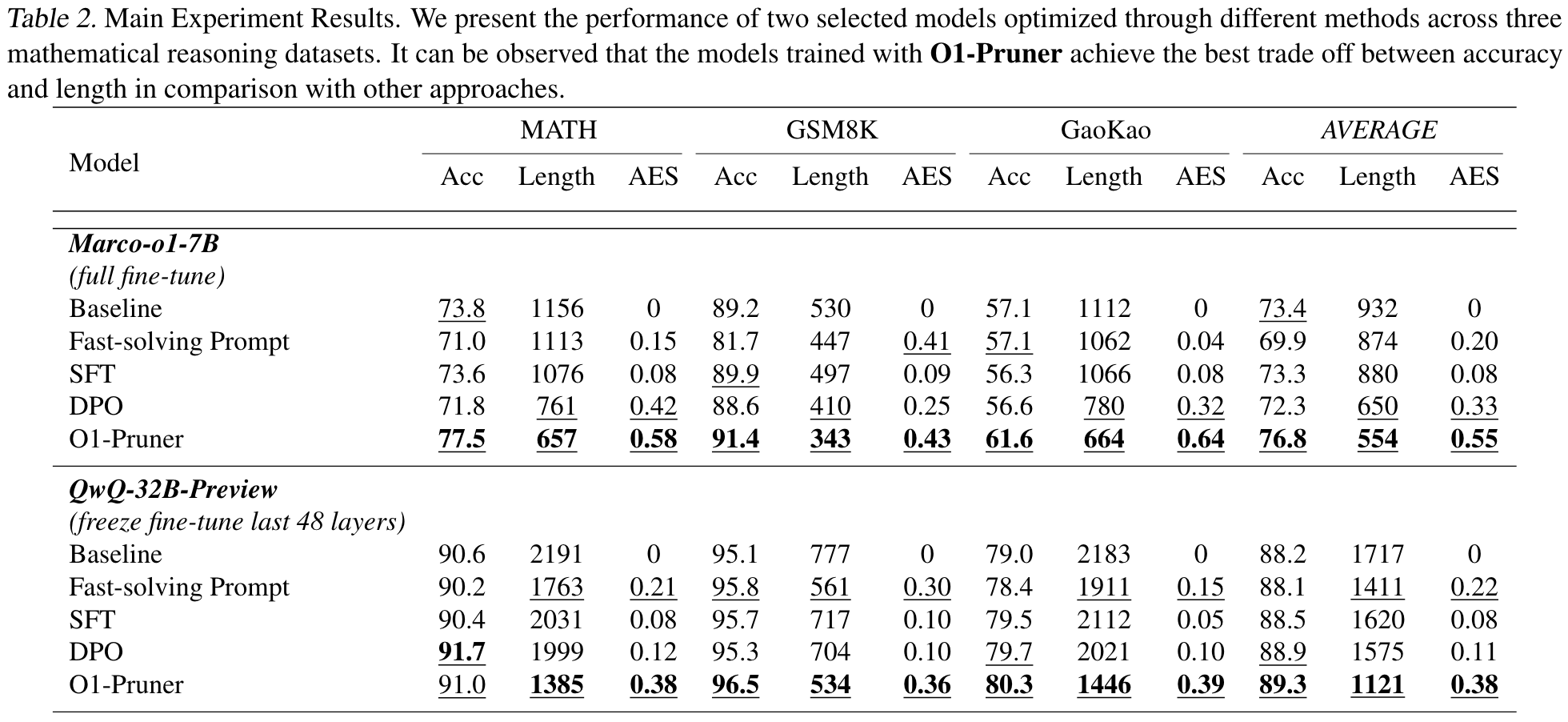
Inference Time-Cost Analysis

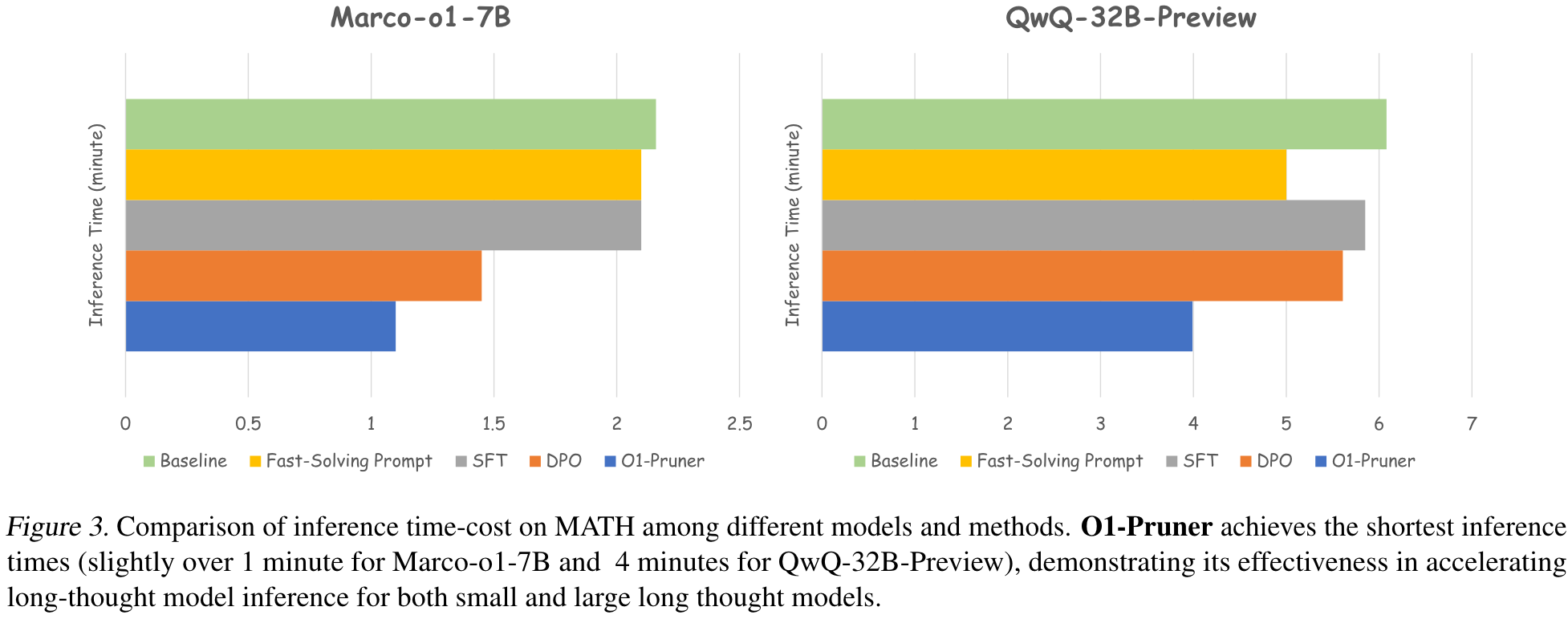
Abalatoin Study

We select several different values of $\lambda(\lambda=0,1,2,5)$ and evaluate the model accordingly.

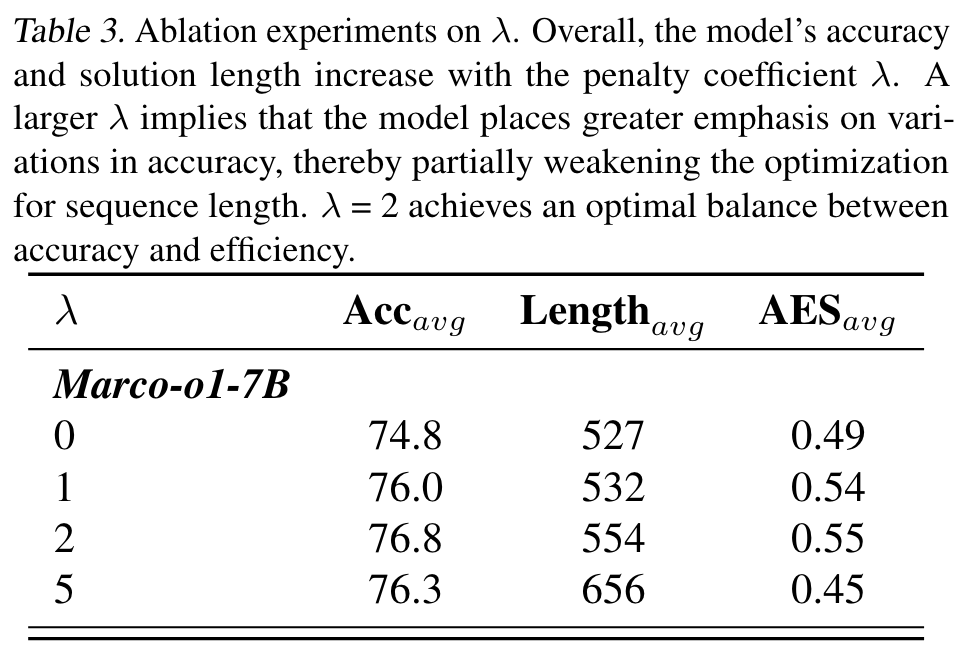
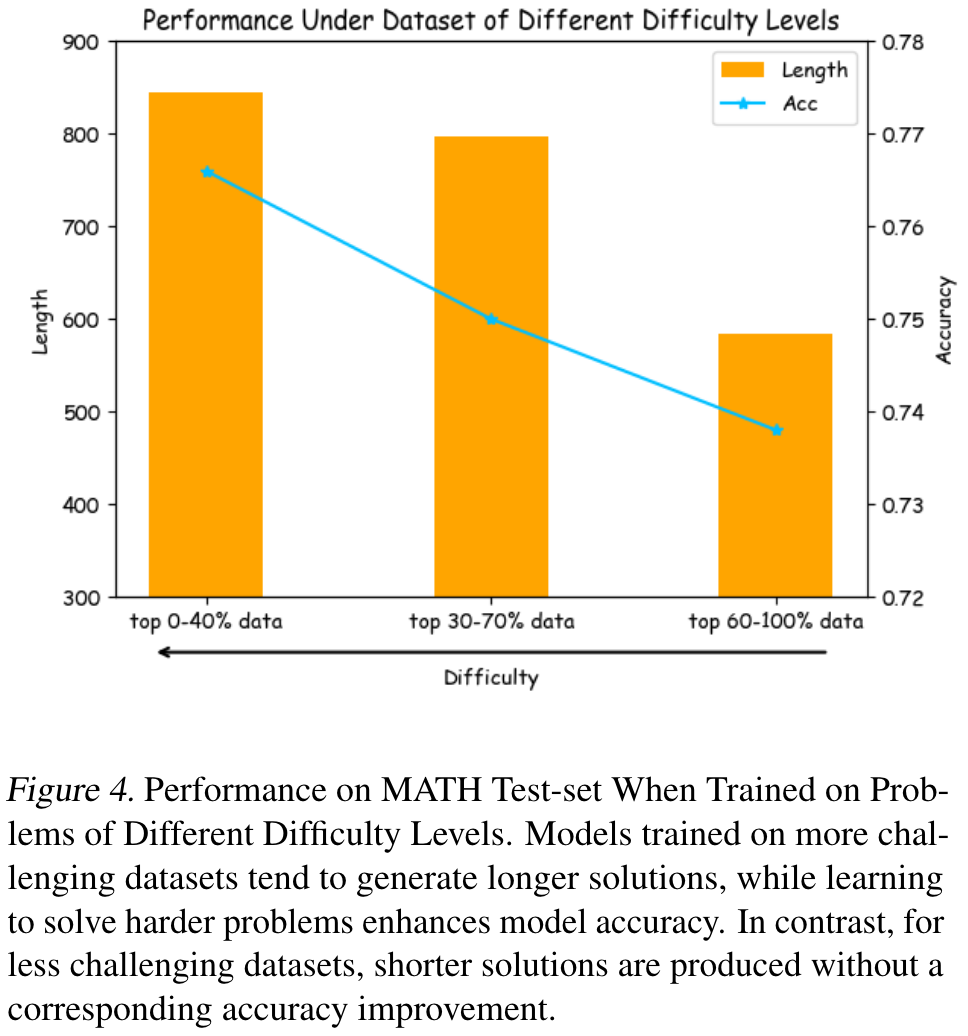
Ablation on Difficulty Levels.

🤖

Others