Raise the Ceiling: Clip-Higher

Cite from: DAPO: An Open-Source LLM Reinforcement Learning System at Scale

In our initial experiments using naive PPO or GRPO, we observed the entropy collapse phenomenon: the entropy of the policy decreases quickly as training progresses. The sampled responses of certain groups tend to be nearly identical. This limited exploration and early deterministic policy, which can hinder the scaling process.

We propose the Clip-Higher strategy to address this issue. Clipping over the importance sampling ratio is introduced in Clipped Proximal Policy Optimization (PPO-Clip) to restrict the trust region and enhance the stability of RL. We identify that the upper clip can restrict the exploration of the policy, where making an 'exploitation' token more probable is much easier yet the probability of an unlikely 'exploration' token is too tightly bounded to bu uplifted.

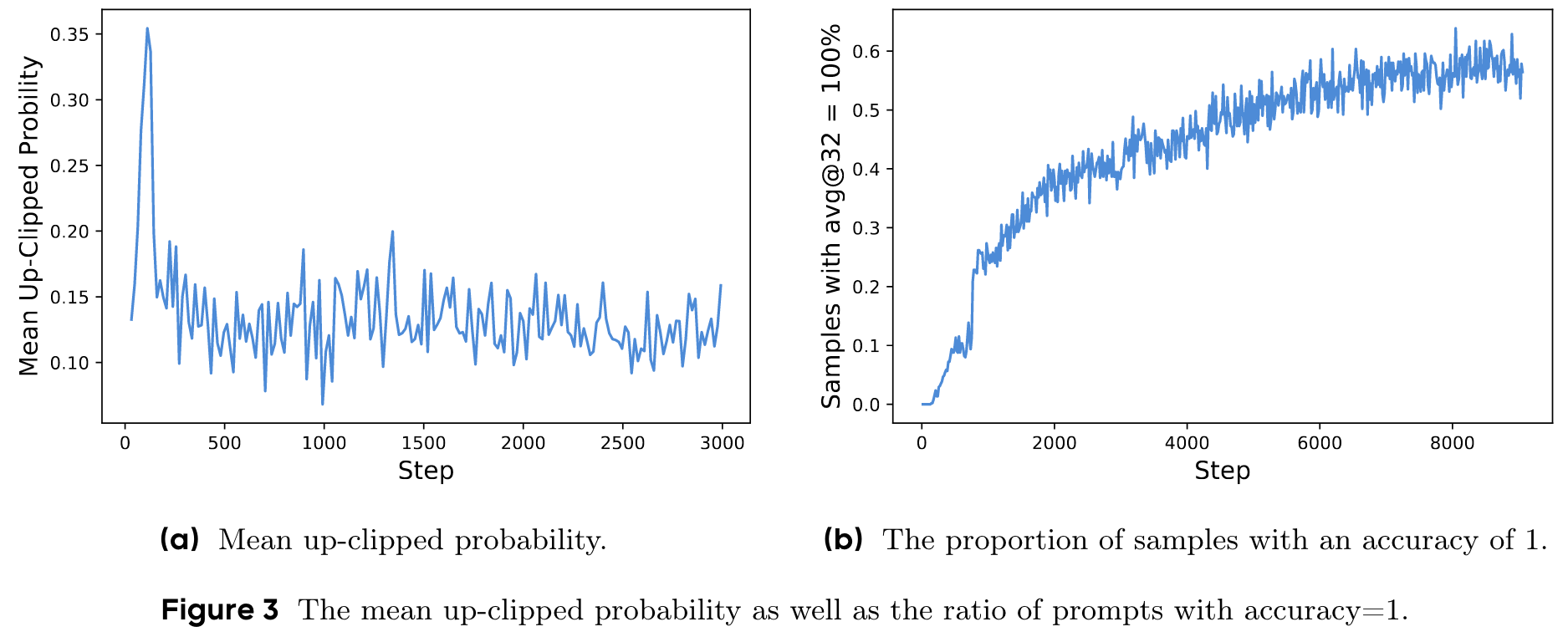
Concretely, when $\varepsilon = 0.2$ (the default value of most algorithms) and $\hat{A}_{i,t} > 0$ (the system tries to increase the probability), consider two actions with probabilities $\pi_{\theta_{\text{old}}}(o_i \mid q) = 0.01$ and $0.9$. The upper bounds of the increased probabilities $\pi_\theta(o_i \mid q)$ are $0.012$ and $1.08$, respectively ($\pi_{\theta_{\text{old}}} \cdot (1 + \varepsilon)$). This implies that 'exploitation' tokens with a higher probability (e.g., $0.9$) are not constrained to get even extremely larger probabilities like $0.999$. Conversely, for low-probability 'exploration' tokens, achieving a non-trivial increase in probability is considerably more challenging. Empirically, we also observe that the mean probability of up-clipped tokens is low: $\pi_\theta(o_i \mid q) < 0.2$ (Figure 3a). This finding supports our intuition that the upper clipping threshold indeed restricts the probability increase of low-probability 'exploration' tokens, thereby potentially constraining the exploration of the system.

Adhering to the Clip-Higher strategy, we decouple the lower and higher clipping range as $\varepsilon_{\text{low}}$ and $\varepsilon_{\text{high}}$, as highlighted in Equation 10:

We increase the value of $\varepsilon_{\text{high}}$ to leave more room for the increase of low-probability tokens. As shown in Figure 2, this adjustment effectively enhances the policy's entropy and facilitates the generation of more diverse samples. We keep $\varepsilon_{\text{low}}$ as it is, because increasing it will suppress the probability of these tokens to 0, resulting in the collapse of the sampling space.