Resource Info
Paper http://arxiv.org/abs/2502.01456
Code & Data https://github.com/PRIME-RL/PRIME
Public arXiv
Date 2025.09.09

Resource	Info
Paper	http://arxiv.org/abs/2502.01456
Code & Data	https://github.com/PRIME-RL/PRIME
Public	arXiv
Date	2025.09.09

Summary Overview

论文介绍了一种名为PRIME的新方法，用于改进强化学习训练。研究指出，稠密的过程奖励在大语言模型推理时间扩展方面比稀疏的结果奖励更加有效，特别是在需要复杂多步的推理任务中。虽然稠密奖励在强化学习中具有解决训练效率和信用分配等问题具有潜力，却面临着在线训练PRM的挑战：收集高质量过程标签成本极高，模型容易受到 reward hacking。

未来解决这些问题，作者提出了PRIME(通过隐式奖励的过程强化学习)方法，其核心创新是仅使用策略输出和结果标签，通过隐式的过程奖励实现对于PRM的更新。实验结果显示，基于Qwen2.5-Math-7B-Base模型，PRIME在多个关键推理基准测试中平均提升15.1%，最终模型Eurus-2-7B-PRIME仅使用10%的训练数据就在7个推理基准测试中超越了Qwen2.5-Math-7B-Instruct，为大模型的强化学习训练提供了新的方法，解决方案。

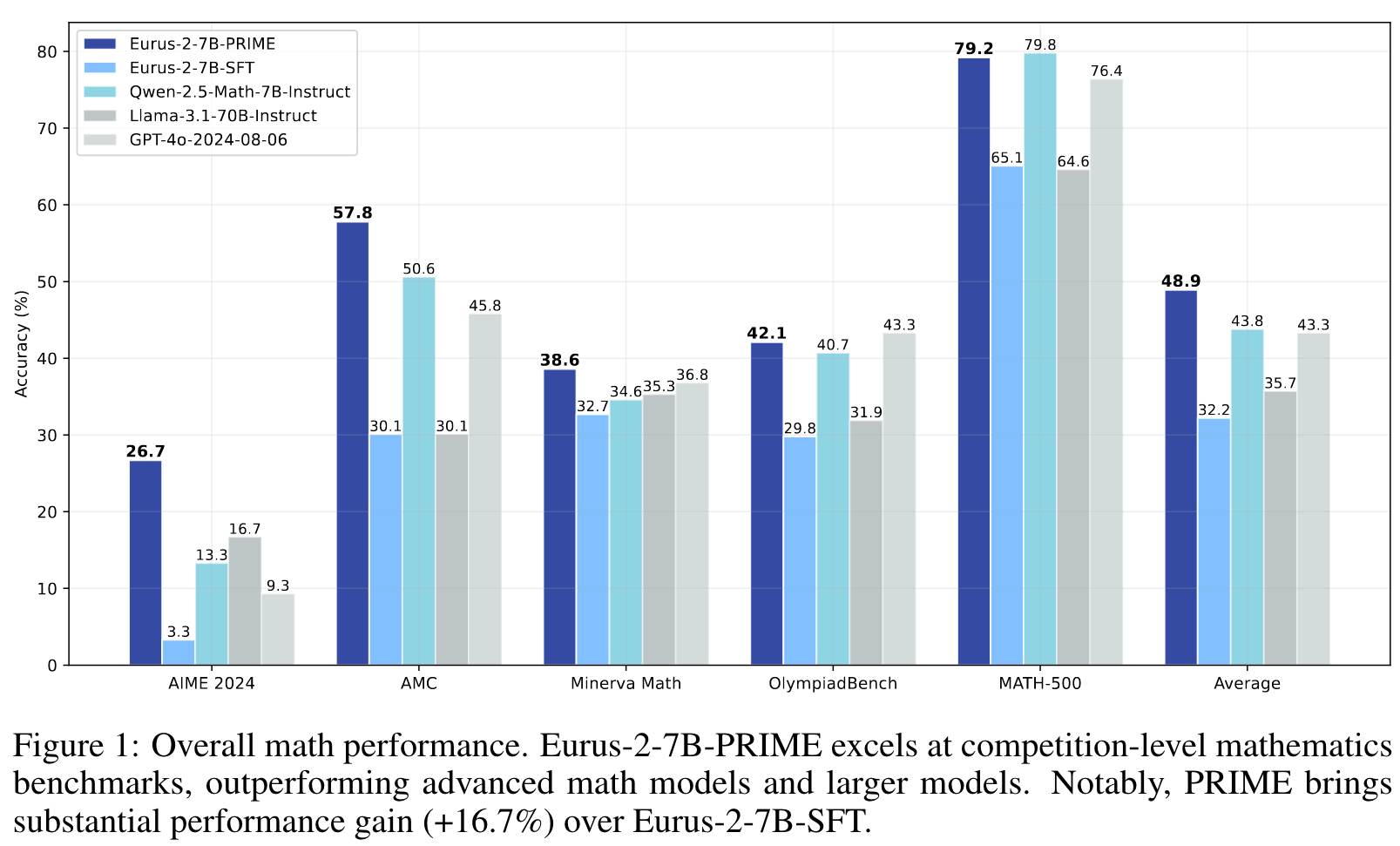
Main Content

Dense process rewards, which provide feedback at each intermediate step rather than only the whole trajectory, have proven effective in inference-time scaling of large language models (LLMs) on challenging reasoning tasks.

how to acquire and utilize high-quality dense rewards at scale?

PRIME:

serves as a general method to fuse token-level dense rewards and sparse outcome rewards by calculating their returns separately before summing together, which is compatible with diverse RL algorithms
eliminates the dedicated reward modeling stage, which is required by existing works, by simply initializing from the SFT model or even the base model.

Key challenges in scalable dense rewards:

Process rewards are hard to define
PRM online updates are not scalable
Explicit reward modeling brings extra cost

r_{\phi}:=\beta\log\frac{\pi_{\phi}(y_t|\mathbf{y}<t)}{\pi_{\text{ref}}(y_t|\mathbf{y}<t)}

In PRIME, upon rollouts being generated and graded by the (ground truth) outcome verifier, we update the Implicit PRM online with on-policy rollouts and outcome supervision and then calculate token-level dense rewards to estimate advantages.

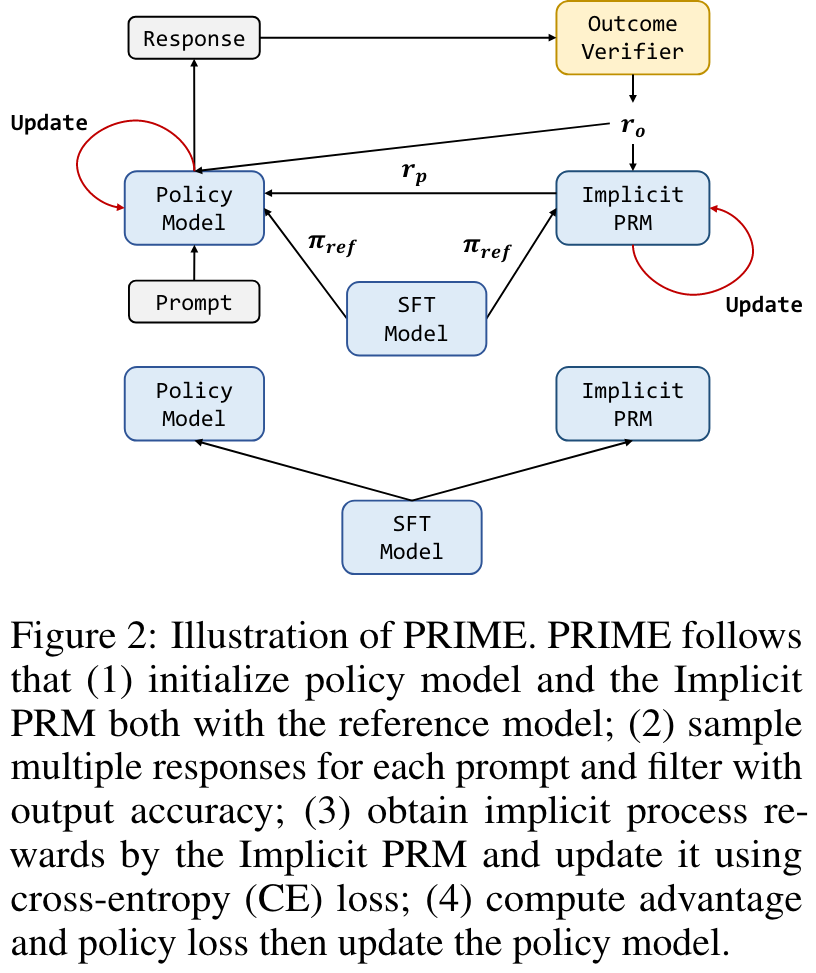
More specifically, we use an Implicit PRM $\pi_\phi$ and an outcome verifier or reward model $r_o$ . We calculate the return of implicit process rewards and outcome rewards separately if both are available, since directly mixing their values may lead to numerical instability. For implicit process rewards, we perform a three-step proces to calculate return: (1) Use the averaged implicit process rewards to calculate the leave-one-out baseline; (2) Normalize the process reward at step $t$ by subtracting the baseline; (3) Calculate the discounted return for each response. For outcome rewards, we directly adopt RLOO without any modification. Finally, the advantage is set to the combination of both returns:

A_t^i = \sum_{s=t}^{|\mathbf{y}^i|} \gamma^{s-t} \cdot \underbrace{\left[ r_\phi(y_s^i) - \frac{1}{K-1} \sum_{j \neq i} r_\phi(y^j) \right]}_{\text{RLOO with implicit process rewards}} + \underbrace{r_o(y^i) - \frac{1}{K-1} \sum_{j \neq i} r_o(y^j)}_{\text{RLOO with outcome rewards}}

Updating policy with PPO clip surrogate loss. We adopt PPO clip surrogate loss for more stable policy updates:

L_{\text{CLIP}}(\theta) = \mathbb{E}_t \left[ \min \left( \frac{\pi_\theta(y_t|\mathbf{y}_{<t})}{\pi_{\theta_{\text{old}}}(y_t|\mathbf{y}_{<t})} A_t, \text{clip}\left(\frac{\pi_\theta(y_t|\mathbf{y}_{<t})}{\pi_{\theta_{\text{old}}}(y_t|\mathbf{y}_{<t})}, 1-\varepsilon, 1+\varepsilon\right) A_t \right) \right]

Online Prompt Filtering. As we sample multiple trajectories for each prompt, we introduce online prompt filtering for each prompt, we introduce online prompt filtering which a certain accuracy range. This (1) preserves only the prompts within a certain median-level difficulty range and (2) balances data distribution for the Implicit PRM online training.

Rule-based Outcome Verifier. Consistent with recent research that adopts exact match with ground truth as unhackable rewards, we define the rule-based ground truth outcome verifiers (OV) for math and coding as follows:

r_o^{\text{math}}(\mathbf{y}) = \begin{cases} 1, & \text{matched} \\ 0, & \text{otherwise} \end{cases} \quad r_o^{\text{code}}(\mathbf{y}) = \frac{\sum \#\text{passes}}{\sum \#\text{test cases}}

🤖

PRIME论文深度分析与创新研究方案

1. 论文的创新之处与独特性

核心创新点

隐式过程奖励机制

提出了PRIME（Process Reinforcement through IMplicit rEwards）框架，通过隐式过程奖励模型（Implicit PRM）实现了仅使用结果标签训练密集奖励模型的突破
解决了传统过程奖励模型需要昂贵的步骤级标注的核心痛点

在线奖励模型更新

实现了过程奖励模型的在线更新，有效缓解了奖励黑客攻击（reward hacking）问题
与传统需要离线训练专门奖励模型的方法相比，大幅降低了开发成本

通用性框架设计

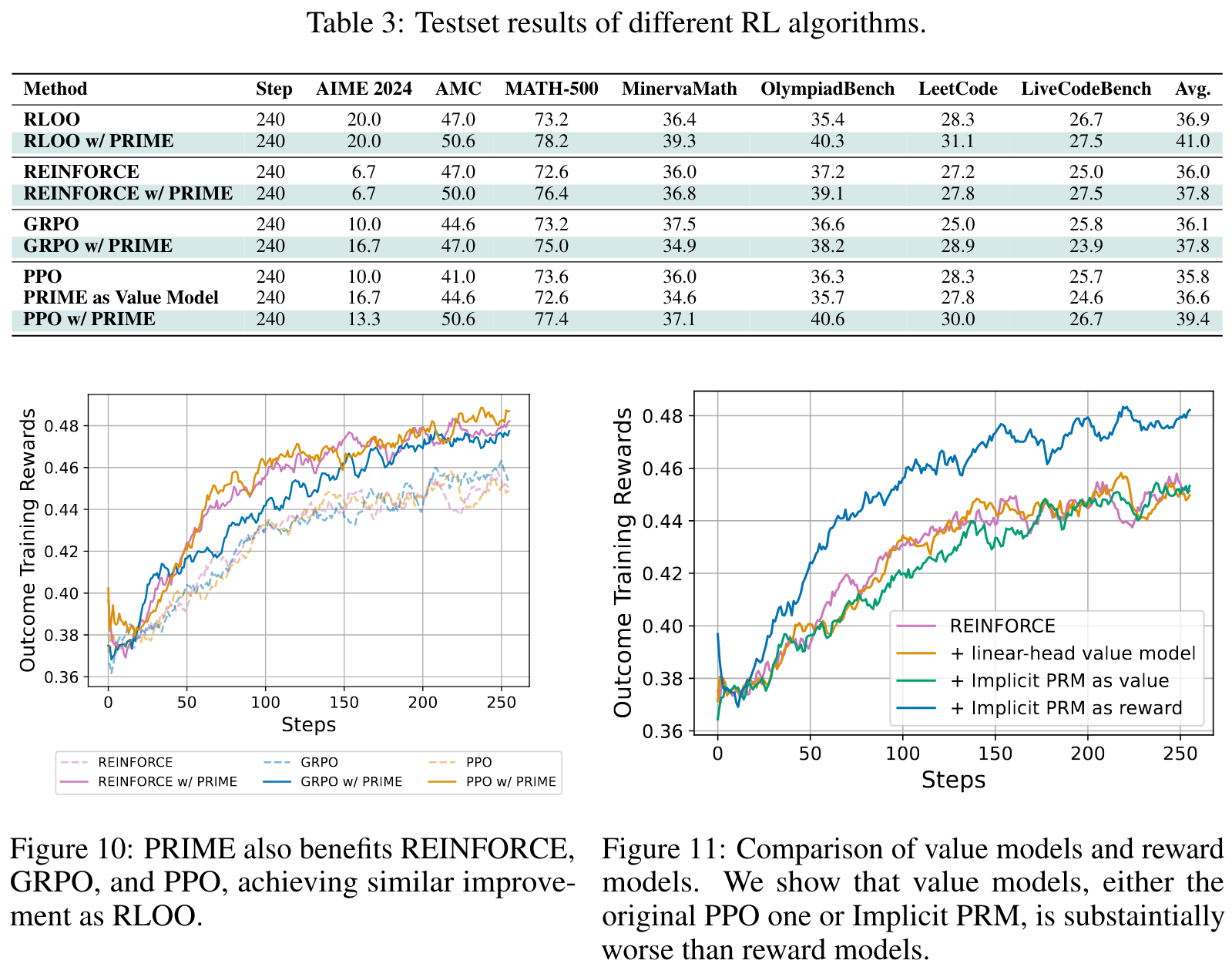
提供了一个通用框架，可以与多种RL算法（RLOO、REINFORCE、PPO、GRPO）无缝集成
支持从SFT模型甚至基础模型直接初始化，消除了专门的奖励建模阶段

关键学习点

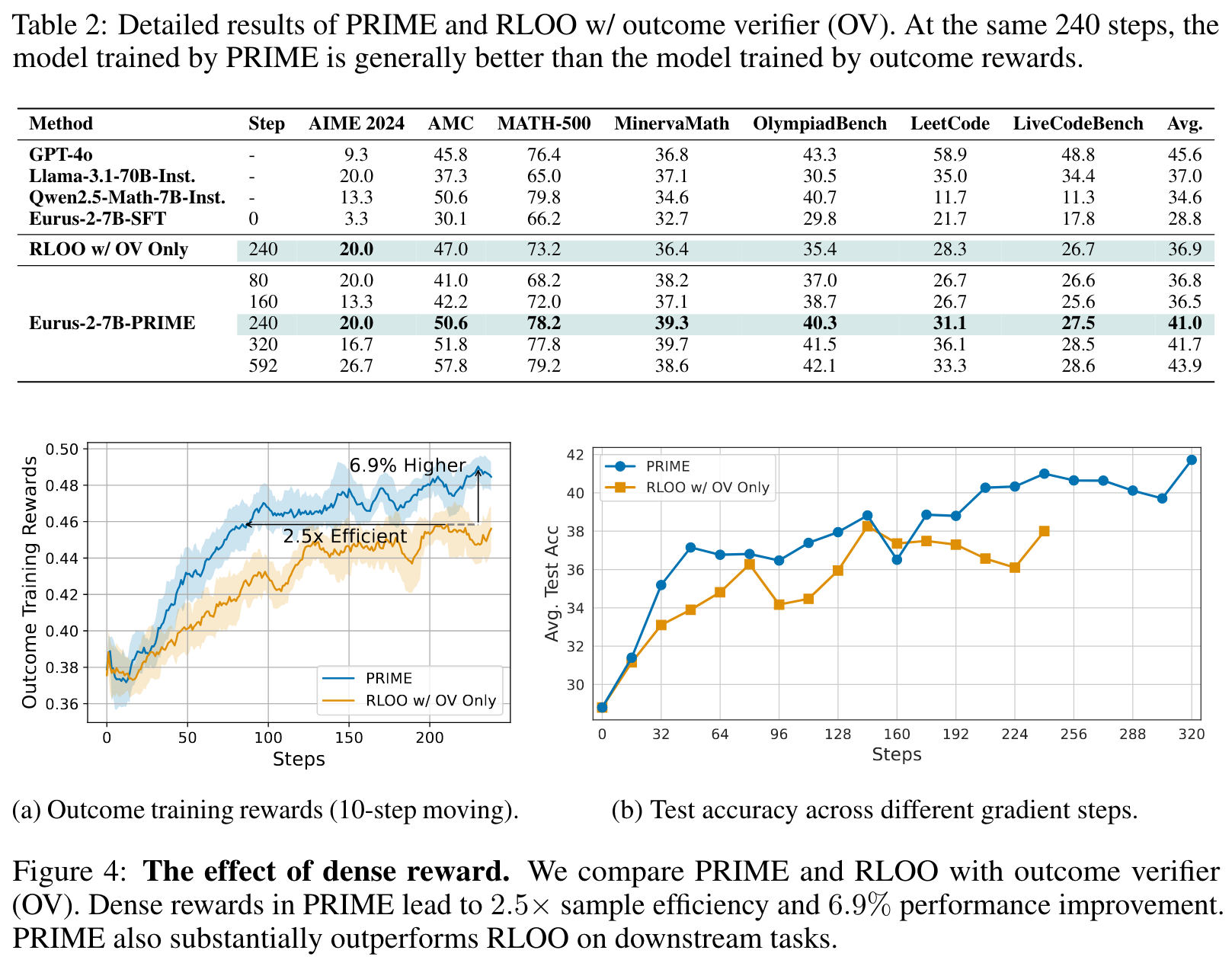
密集奖励的重要性：在复杂推理任务中，token级别的密集奖励相比稀疏的结果奖励能显著提升样本效率（2.5倍）和最终性能（6.9%）
在线更新的必要性：实验证明在线更新PRM对防止过度优化至关重要，离线PRM会因分布偏移而逐渐失效
初始化策略的影响：直接使用SFT模型初始化PRM比使用专门训练的PRM效果更好，这揭示了分布对齐的重要性

2. 论文中存在的问题及改进建议

主要问题

实验规模限制

主要在7B参数模型上验证，缺乏大规模模型（如70B+）的系统性验证
RL训练数据相对有限（150K queries × 4 samples），可能限制了方法的全面评估

理论分析不足

缺乏对隐式过程奖励收敛性的理论保证
未深入分析为什么隐式PRM作为奖励模型比作为价值模型效果更好的理论原因

评估基准局限

主要集中在数学和编程任务，缺乏其他推理密集型任务的验证
缺乏与人类评估的对比，仅依赖自动化指标

改进建议

扩展实验规模：在更大参数量模型和更多样化任务上验证方法的普适性
理论分析补强：提供隐式过程奖励的收敛性分析和最优性理论保证
评估体系完善：引入人类评估和更多元化的评估基准
计算效率优化：研究如何进一步降低在线更新的计算开销

3. 基于论文的内容和研究结果，提出的创新点或研究路径

创新点1：多模态隐式过程奖励学习

将PRIME框架扩展到多模态推理任务，特别是数学几何问题和科学推理中涉及图表、公式的复杂场景。

创新点2：层次化隐式奖励结构

设计多层次的隐式奖励机制，在不同抽象层次（token级、步骤级、子问题级）提供奖励信号，实现更精细的信用分配。

创新点3：对抗性隐式奖励鲁棒性

研究隐式过程奖励在对抗性环境下的鲁棒性，开发能够抵抗奖励污染和分布攻击的强化学习框架。

创新点4：自适应隐式奖励权重调节

开发动态调节过程奖励和结果奖励权重的机制，根据任务复杂度和学习阶段自适应调整奖励结构。

4. 为新的研究路径制定的研究方案

研究方案1：多模态隐式过程奖励学习

研究目标

开发支持视觉-文本联合推理的多模态隐式过程奖励机制，提升模型在几何证明、科学实验分析等任务上的表现。

研究方法

阶段一：多模态隐式奖励建模

扩展隐式PRM架构，集成视觉编码器处理图像信息
设计跨模态注意力机制，实现视觉和文本信息的有效融合
开发多模态奖励计算公式： $r_mm(v_t, y_t) = β log π_φ(y_t|v_{<t}, y_{<t}) / π_ref(y_t|v_{<t}, y_{<t})$

阶段二：多模态数据集构建

收集包含图表、几何图形的数学问题（目标：50K样本）
构建科学实验推理数据集，包含实验图片和推理过程
设计多模态标注框架，确保视觉-文本对齐质量

阶段三：训练与优化

实现多模态PRIME框架，支持视觉输入的在线奖励更新
对比单模态和多模态方法在几何推理、科学问题解决上的效果
分析不同模态信息对奖励信号的贡献度

预期成果

在几何证明任务上相比单模态方法提升15-20%准确率
发表顶级会议论文（ICLR/NeurIPS）
开源多模态隐式奖励学习框架

研究方案2：层次化隐式奖励结构

研究目标

构建多层次隐式奖励机制，在token、步骤、子问题等不同粒度提供奖励信号，实现更精确的信用分配。

研究方法

阶段一：层次化奖励架构设计

定义三层奖励结构：
- Token级：r_token(y_t) = β_1 log π_φ1(y_t|y_{<t}) / π_ref(y_t|y_{<t})
- 步骤级：r_step(s_i) = β_2 log π_φ2(s_i|s_{<i}) / π_ref(s_i|s_{<i})
- 子问题级：r_subproblem(p_j) = β_3 log π_φ3(p_j|p_{<j}) / π_ref(p_j|p_{<j})
设计层次化注意力机制，实现不同层次间的信息传递

阶段二：自动分解算法

开发基于语义分析的自动步骤分割算法
设计子问题识别机制，基于依赖关系图进行问题分解
构建层次化标注工具，支持多粒度标注

阶段三：联合优化策略

设计多层次奖励的联合优化目标函数
实现层次化优势估计算法
开发自适应权重调节机制，平衡不同层次奖励的影响

预期成果

在复杂推理任务上实现20-25%的性能提升
显著改善长序列推理的信用分配问题
提供层次化奖励学习的理论分析框架

研究方案3：对抗性隐式奖励鲁棒性

研究目标

研究隐式过程奖励在对抗性环境下的鲁棒性，开发抵抗奖励污染和分布攻击的强化学习方法。

研究方法

阶段一：对抗性攻击建模

定义奖励污染攻击：恶意修改训练数据中的奖励标签
设计分布偏移攻击：构造与训练分布差异较大的测试样本
开发梯度攻击：通过梯度信息构造对抗性样本

阶段二：鲁棒性防御机制

设计基于不确定性估计的奖励过滤机制
开发多模型集成的鲁棒奖励估计方法
实现基于对抗训练的隐式PRM训练策略

阶段三：理论分析与验证

提供鲁棒性的理论保证和收敛性分析
在多种攻击场景下验证防御效果
分析计算开销与鲁棒性的权衡关系

预期成果

在对抗性环境下保持80%以上的原始性能
提供隐式奖励鲁棒性的理论框架
开发实用的对抗性强化学习工具包

研究方案4：自适应隐式奖励权重调节

研究目标

开发动态调节过程奖励和结果奖励权重的自适应机制，根据任务特性和学习进度优化奖励结构。

研究方法

阶段一：权重调节策略设计

基于任务复杂度的权重初始化：w_process = f(complexity_score)
基于学习进度的动态调节：w_t = w_{t-1} + α * gradient_signal
基于性能反馈的自适应更新：w_new = argmax_w E[performance|w]

阶段二：复杂度评估机制

设计多维度任务复杂度评估指标
开发基于图神经网络的问题难度预测模型
构建任务特征与最优权重的映射关系

阶段三：在线学习算法

实现基于强化学习的权重调节策略
设计多臂老虎机方法进行权重探索
开发元学习框架，快速适应新任务的权重配置

预期成果

在不同复杂度任务上实现10-15%的平均性能提升
显著减少超参数调优的人工成本
提供自适应奖励学习的通用框架

这些研究方案基于PRIME的核心思想，在不同维度上进行创新扩展，既保持了原方法的优势，又解决了现有方法的局限性，具有重要的理论价值和实用意义。

目录

Summary Overview

Main Content

🤖

PRIME论文深度分析与创新研究方案

1. 论文的创新之处与独特性

核心创新点

关键学习点

2. 论文中存在的问题及改进建议

主要问题

改进建议

3. 基于论文的内容和研究结果，提出的创新点或研究路径

创新点1：多模态隐式过程奖励学习

创新点2：层次化隐式奖励结构

创新点3：对抗性隐式奖励鲁棒性

创新点4：自适应隐式奖励权重调节

4. 为新的研究路径制定的研究方案

研究方案1：多模态隐式过程奖励学习

研究目标

研究方法

预期成果

研究方案2：层次化隐式奖励结构

研究目标

研究方法

预期成果

研究方案3：对抗性隐式奖励鲁棒性

研究目标

研究方法

预期成果

研究方案4：自适应隐式奖励权重调节

研究目标

研究方法

预期成果

Others