请注意,本文编写于 765 天前,最后修改于 765 天前,其中某些信息可能已经过时。
圆周长公式推导
前几天看到有人再群里说如何推导 C=2πr,自己私下推导了一下。当然有些微积分的公式也忘了,群里求助了一些考研同学的帮助😂,本人数学废物实锤了。
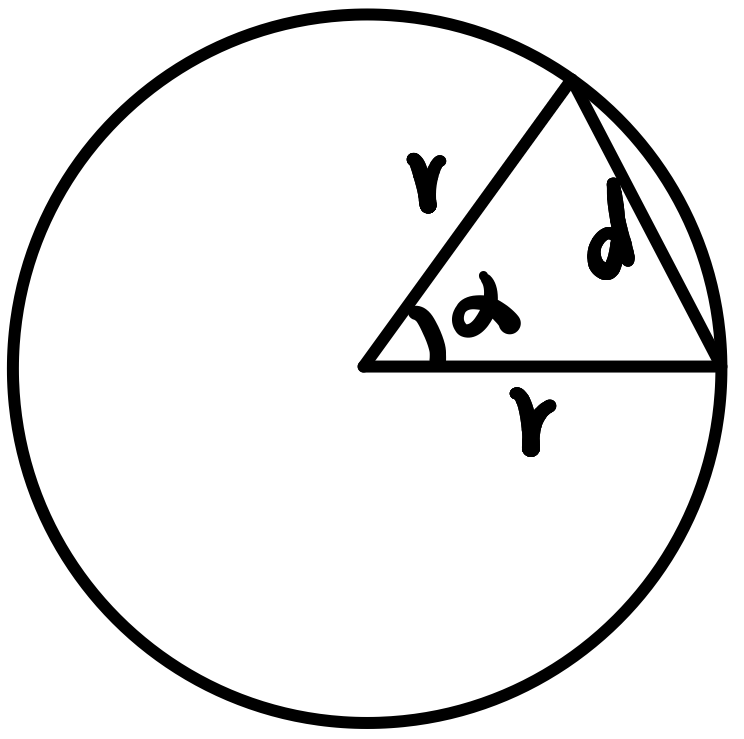
-
根据余弦公式有d2=r2+r2−2r2cosα,则d=r2(1−cosα)
-
多边形周长:C=α2πd=α2πr2(1−cosα)
-
圆的周长:C=limα→0+α2πr2(1−cosα)
-
计算:limα→0+α2(1−cosα)
1−cosα=1−(cos22α−sin22α)=2sin22α=2sin2α(∵sin2α>0)
limα→0+α2(1−cosα)=limα→0+α2sin2α=limα→0+2×1(sin2α)′=limα→0+2×121cos2α=1
-
再带入上式可得 C=2πr
本文作者:Geaming
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA
许可协议。转载请注明出处!

