Resource	Info
Paper	http://arxiv.org/abs/2505.18454
Code & Data	https://github.com/Yueeeeeeee/HRPO
Public	arXiv
Date	2025.07.10

Main Content

作者提出了针对于 latent reasoning 的 RL 算法 (HRPO)。

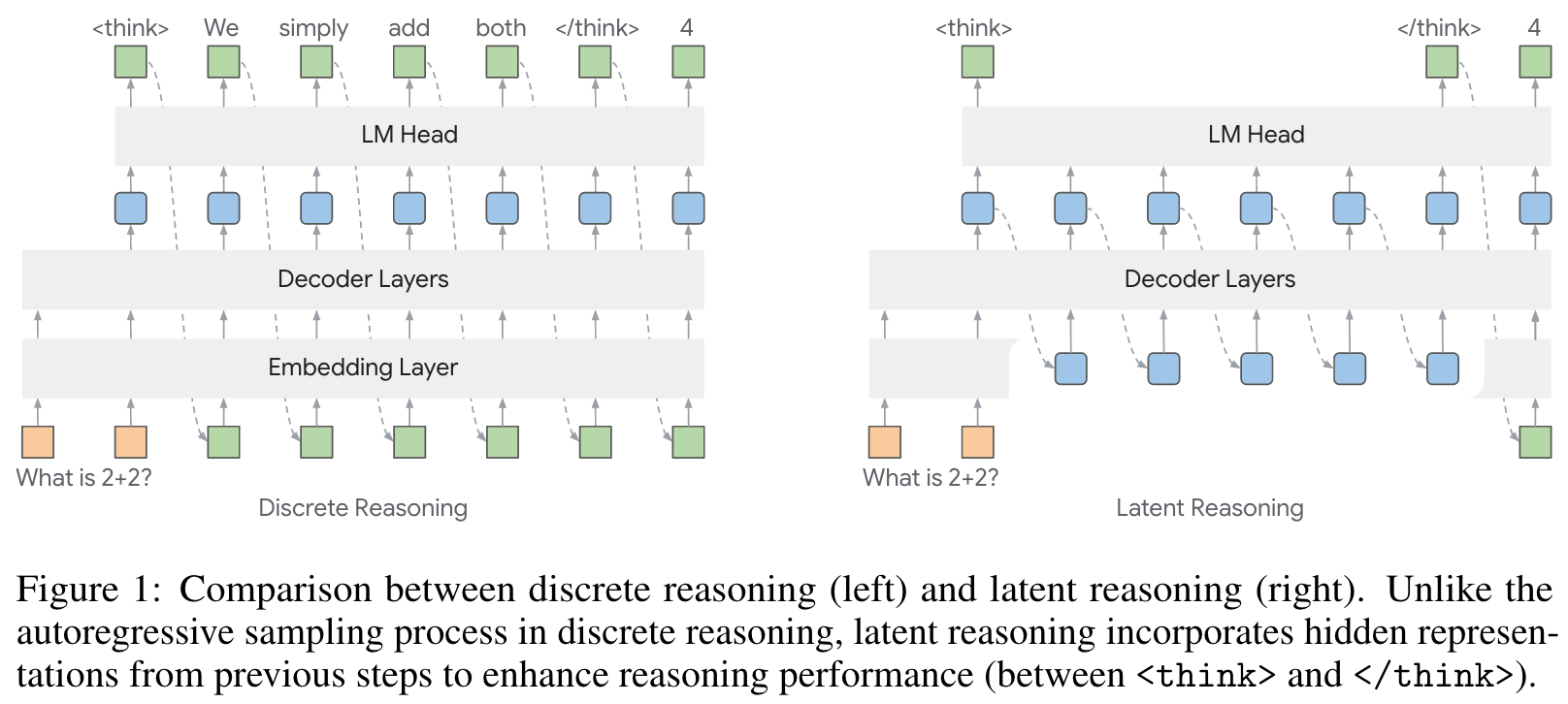
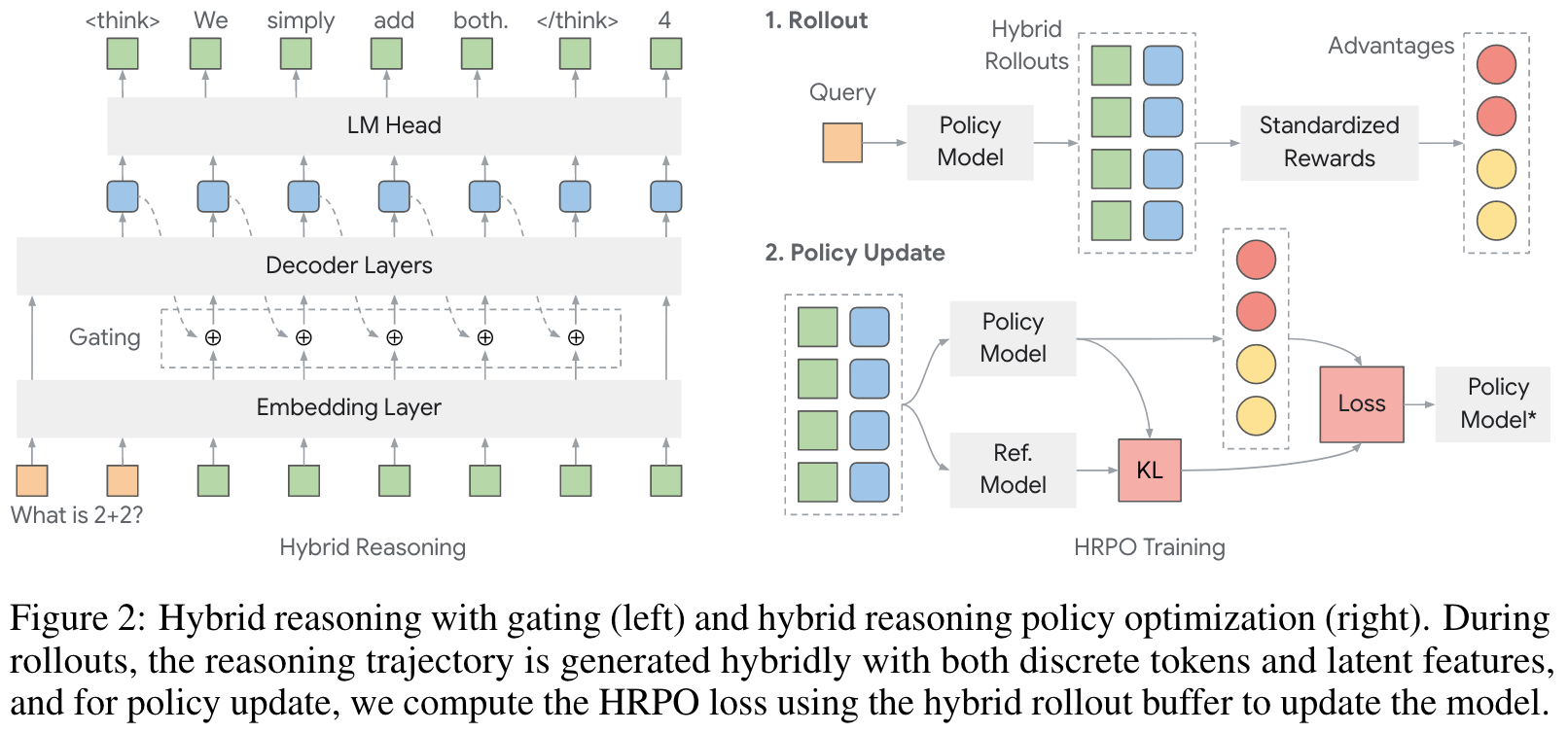
We first describe our notation and settings for hybird latent reasoning. For input query $x=[x_1,x_2,\cdots,x_t]$ and its corresponding token embeddings $E=[e_1,e_2,\cdots,e_t]$, we describe the raw hidden states from the LLM output at step $t$ with $\hat{h}_t$, namely:

in which $\texttt{Transformer}$ denotes the transformer model (i.e., decoder layers), $\hat{H}$ represents the final-layer hidden states produced by the $\texttt{Transformer}$. With the LM head ($\texttt{Head}$), the next output token $\hat{x}_{t+1}$ can be sampled from the output distribution over the vocabulary via:

However, hidden states often lie outside the model's token embedding manifold, which degrades generation quality when fed directly. To avoid this, we project $\hat{h}_t$ back into the embedding space to ensure the inputs conform to the model's learned distribution. Specifically, we use the output probabilities $p_{t+1}$ to compute a weighted interpolation over the vocabulary:

in which $\tau$ is the temperature and $W_e$ denotes the embedding matrix of the LLM. In other words, we compute the next input embeddingg as a weighted sum of all token embeddings, with weights given by $p_{t+1}$. In addition, $p_{t+1}$ is normalized to preserve the scale and variance of the output vector. This sampling-free mapping ensures differentiability and aligns the projected embedding with the model's native input space, thus leading to improved training dynamics.

While interpolated embeddings preserve semantic continuity, directly feeding $h_{t+1}$ as the next token input removes stochasticity and injects noise from irrelevant tokens, causing degraded generation within RL rollouts. As such, we design a hybird approach for latent reasoning by gradually imposing hidden state representations into the sampled token embeddings with a gating mechanism. Drawing on gated recurrence models, we formulate the gating mechanism as:

$e_{t+1}$ is the resulting hybird input for the next step, $\hat{e}_{t+1}$ denotes the embedding of the sampled discrete token $\hat{x}_{t+1}$, whereas $h_{t+1}$ is the projected hidden states. The gates $r_t$ and $i_t$ leverages sigmoid function $\sigma$ to control the blending, $a_t$ scales $\hat{e}_{t+1}$, $c$ is a fixed scaling constant, and $\Lambda$ is a learnable vector. Note that hybird reasoning only applies during the reasoning phase (i.e., $\t\in\texttt{think}$), while the final answer is still generated via standard autoregressive decoding. By initializing $a_t\to1$, the inputs first draw predominantly from the sampled token embeddings, thereby effectively preserving the LLM's generative capabilities. As the training progresses, the value range of $a_t$ converages to an optimum range and thus incorporates informative features from both hidden representations and sampled tokens.

As such, our HRPO implementation remains light weight, strictly on-policy and could be seamlessly combined with further RL optimizations.

Exp 1: open-domain & multi-hop knowledge-intensive question answering (Knowledge)

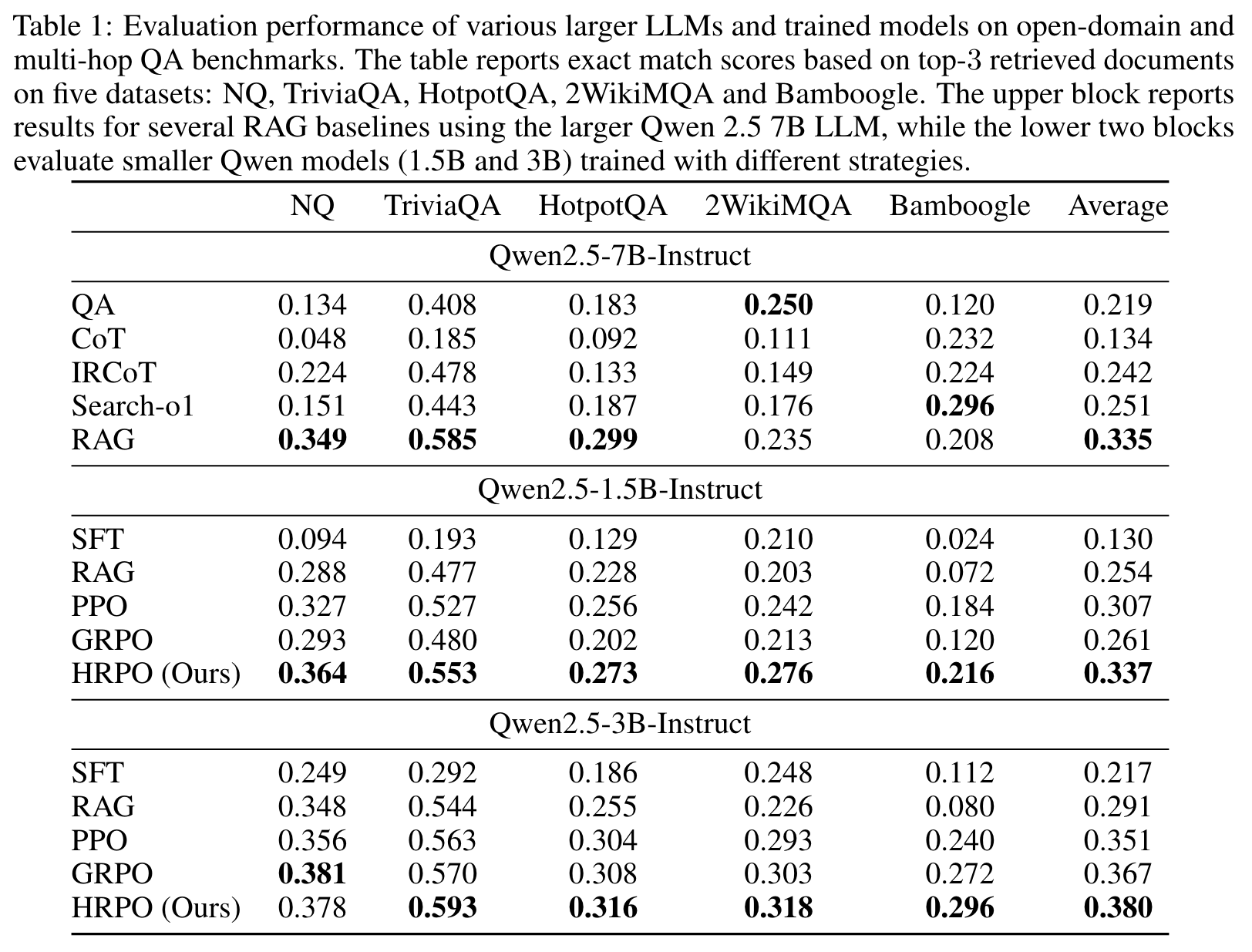
Exp 2: science, technology, engineering or mathematics (STEM) benchmarks.

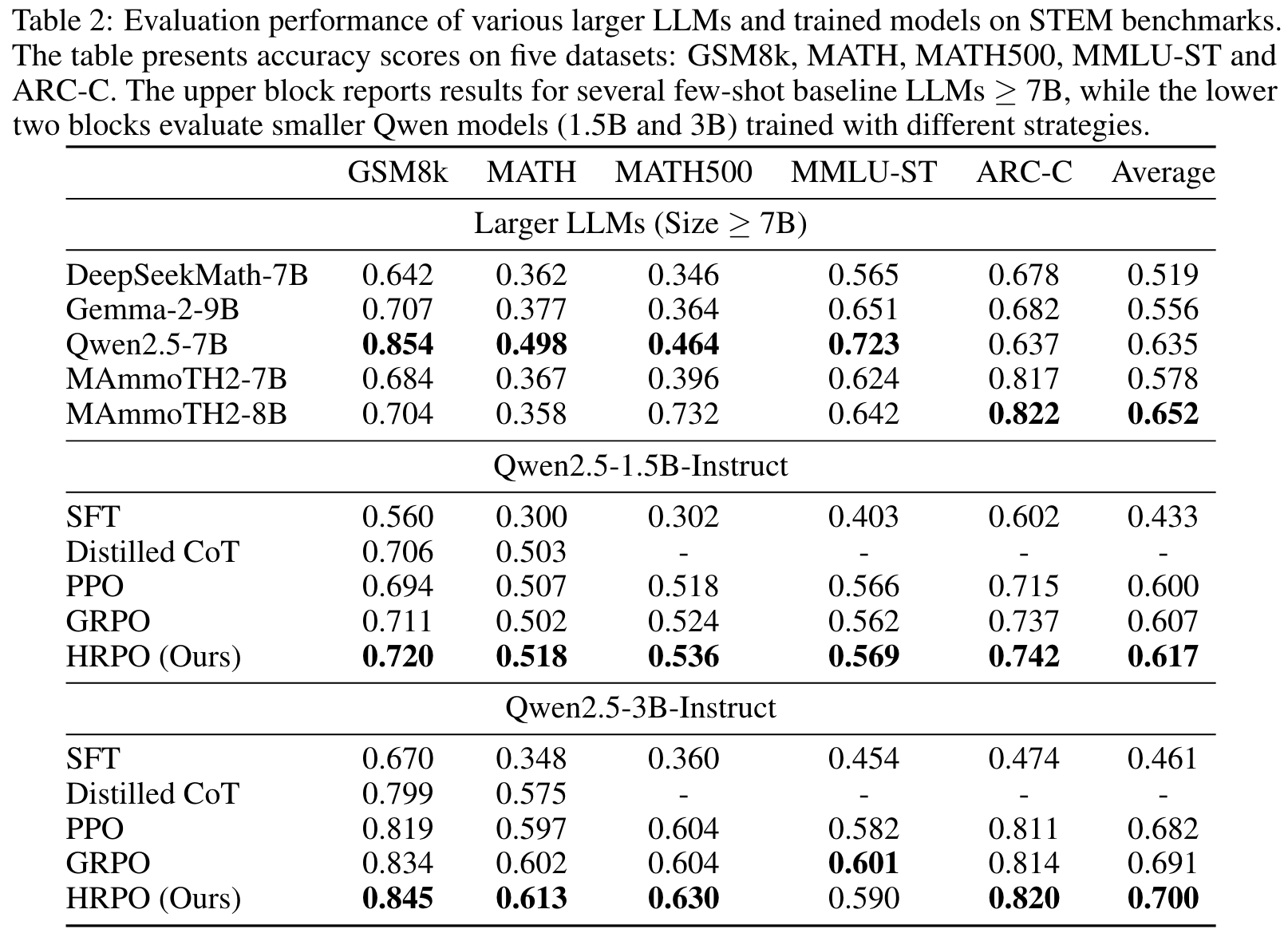
Different Strategies for Latent Reasoning. We compare different strategies to compute latent representations. Specifically, we use three methods to integrate hidden states into RL and train the 1.5B Qwen model on the MATH dataset. These variants are: (1) hidden states, which use the final layer hidden states as the next input; (2) interpolation, which employs interpolated embeddings; and (3) HRPO, our hybird latent reasoning. We visualize the exponential moving average (EMA) of rewards along with the GRPO baseline. Due to the mismatch between hidden states and embeddings, using hidden states degrades generation and yields nonosensical rollouts with zero reward. Although interpolation performs similar to HRPO for the first few hundred steps, the rewards eventually collapse and only slowly recover, likely because interpolation introduces excessive noise. We also provide a direct comparison between HRPO and latent reasoning mehtods. Overall, our approach achieves superior training dynamics with faste convergence while maintaining stability comparable to GRPO, highlighting the efficacy of our hybird design choice in HRPO.

🤖

Others