Resource	Info
Paper	http://arxiv.org/abs/2507.18071
Code & Data	/
Public	arXiv
Date	2025.08.07

Summary Overview

作者认为在 GRPO 中的重要性采样仅仅是在 token-level 进行计算，这样会造成对于 LLM RL 训练的不稳定，尤其是对于 MoE 模型来说。作者重写了重要性采样的计算方式，使其变成 sequence-level 的计算。

Main Content

GRPO 在训练大语言模型时可能会出现训练不稳定的问题，通常会导致模型崩溃等问题。在本文中，作者将这种不稳定醒归结于源于 GRPO 算法中的重要性采样权重的错误使用和无效。这在训练中引入了噪声，并且该噪声会随着响应长度的增加而逐渐积累，并通过裁剪机制进一步扩大，最终导致模型塌陷。

Motivation

The growth in model size, sparsity (e.g., in Mixture-of-Experts models), and response length necessitates a large rollout batch size to maximize hardware utilization during RL. To improve sample efficiency, it is standard practice to partition a large batch of rollout data into multiple mini-batches for gradient updates. This procedure inevitably introduces an off-policy learning setting, where responses $y$ are sampled from an old policy $\pi_\theta$ rather than the current policy $\pi_\theta$ being optimized. This also explains the necessity of the clipping mechanism in PPO and GRPO, which prevents overly "off-policy" samples from being involved in gradient esstimation.

While mechanisms like clipping aim to manage this off-policy discrepancy, we identify a more fundamental issue in GRPO: its objective is ill-posed. This problem becomes particularly acute when training large models on long-response tasks, leading to catastrophic model collapse. The ill-posed nature of the GRPO objective stems from a misapplication of importance sampling weights. The principle of importance sampling is to estimate the expectation of a function $f$ under a target distribution $\pi_\text{bar}$ by re-weighting samples drawn from a behavior distribution $\pi_\text{beh}$:

Crucially, this relies on averaging over multiple samples ($N\gg1$) from the behavior distribution $\pi_\text{beh}$ for the importance weight $\frac{\pi_\text{tar}(z)}{\pi_\text{beh}(z)}$ to effectively correct for the distribution mismatch.

In contrast, GRPO applies the importance weight $\frac{\pi_\theta(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_\text{old}}(y_{i,t}|x,y_{i,<t})}$ at each token position $t$. Since this weight is based on a single sample $y_{i,t}$ from each next-token distribution $\pi_{\theta_\text{old}}(\cdot|x,y_{i,<t})$, it fails to perform the intended distribution-correction role. Instead, it introduces high-variance noise into the training gradients, which accumulates over long sequences and is exacerbated by the clipping mechanism. We have empirically observed that this can lead to model collapse that is often irreversible. Once the collapse occurs, resuming training is unavailing, even when reverting to a previous checkpoint and meticulously tuning hyperparameters (e.g., the clipping ranges), extending generation length, or switching the RL queries.

The above observation suggests a fundamental issue in GRPO's design. The failure of the token-level importance weight points to a core principle: the unit of optimization objective should match the unit of reward. Since the reward is granted to the entire sequence, applying off-policy correction at the token level appears problematic. This motivates us to forego the token-level objective and explore utilizing importance weights and performing optimization directly at the sequence level.

Therefore, GSPO applies clipping to entire responses instead of individual tokens to exclude the overly "off-policy" samples from gradient estimation, which matches both the sequence-level rewarding and optimization.

与 GRPO 不同的是，GSP 对于一个 response 中的所有 token 都使用统一的 weight。

同时，为了丰富的扩展性，作者还提出了一个 token-level 级别的 Loss: GSPO-token.

$\text{sg}[\cdot]$ 代表着停止梯度 (stop the gradient)。

GSPO-token and GSPO are numerically identical in the optimization objective, clipping condition, and theoretical gradient when we set the advantages of all the tokens in the response $y_i$ to the same value (i.e., $\hat{A}_{i,t}=\hat{A}_{i}$), while GSPO-token enjoys the higher flexibility of adjusting the advantages per token.

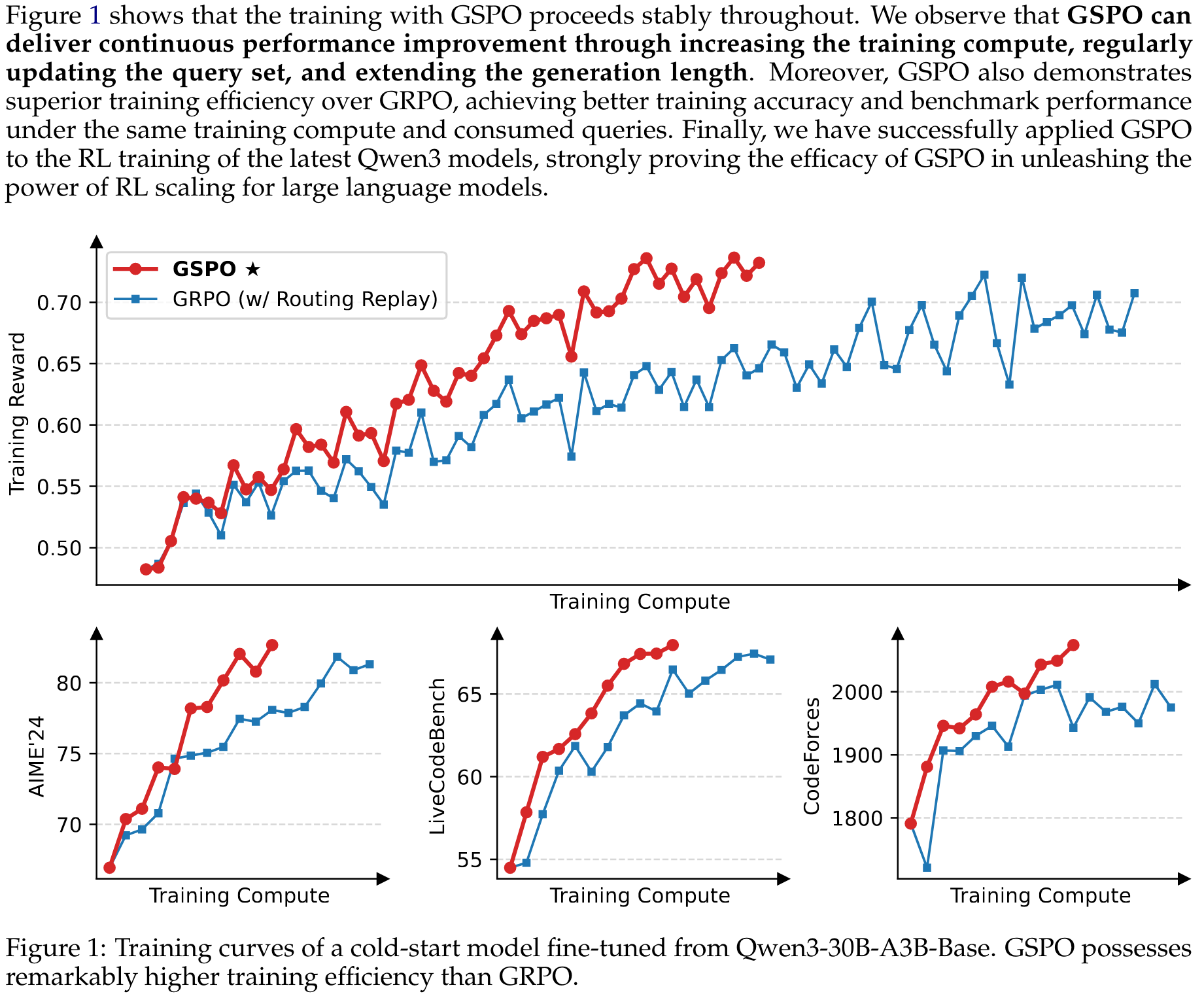
Benefit of GSPO for MoE Training

与密集模型的强化学习训练相比，MoE模型的稀疏激活特性引入了独特的稳定性挑战。特别地，我们发现当采用 GRPO 算法时，MoE模型的 expert-activation volatility 会阻止强化学习训练正常收敛。具体而言，经过一次或多次梯度更新后，针对同一响应激活的专家可能会发生显著变化。例如，对于48层的Qwen3-30B-A3B-Base模型，在每次强化学习梯度更新后，对于同一个rollout样本，新策略$\pi_\theta$下激活的专家与旧策略$\pi_{\theta_{\text{old}}}$下激活的专家大约有10%的差异。这种现象在更深的MoE模型中变得更加突出，使得token级重要性比率$w_{i,t}(\theta) = \frac{\pi_\theta(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t}|x,y_{i,<t})}$剧烈波动并进一步使其失效，如第3节和第4.2节所讨论的，从而阻碍了强化学习训练的正常收敛。

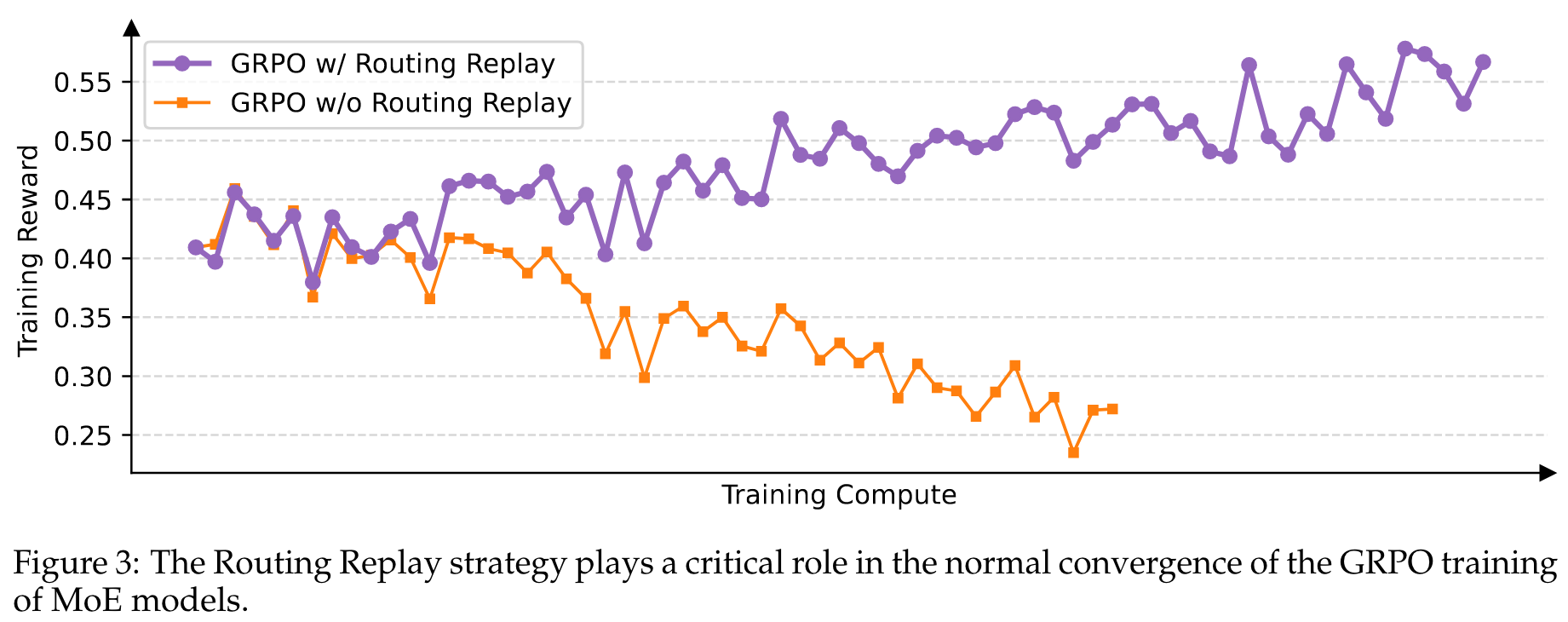
为了解决这一挑战，我们之前采用了 Routing Replay 训练策略。具体而言，我们缓存$\pi_{\theta_{\text{old}}}$中激活的专家，并在计算重要性比率$w_{i,t}(\theta) = \frac{\pi_\theta(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t}|x,y_{i,<t})}$时在$\pi_\theta$中"重放"这些路由模式。通过这种方式，对于每个token $y_{i,t}$，$\pi_\theta(y_{i,t}|x,y_{i,<t})$和$\pi_{\theta_{\text{old}}}(y_{i,t}|x,y_{i,<t})$共享相同的激活网络，从而我们可以恢复token级重要性比率的稳定性，并确保在梯度更新过程中一致激活网络的优化。图3表明路由重放是MoE模型GRPO训练正常收敛的一项关键技术。

The key insight is that GSPO focuses only on the sequence likelihood (i.e., $\pi_\theta(y_i|x)$) and is not sensitive to the individual token likelihood (i.e., $\pi_\theta(y_{i,t}|x,y_{i,<t})$).

🤖

Others