Resource Info
Paper https://arxiv.org/abs/2506.01347
Code & Data https://github.com/TianHongZXY/RLVR-Decomposed
Public arXiv
Date 2025.07.17

Resource	Info
Paper	https://arxiv.org/abs/2506.01347
Code & Data	https://github.com/TianHongZXY/RLVR-Decomposed
Public	arXiv
Date	2025.07.17

Summary Overview

作者讨论了在强化学习中正样本和负样本对于训练的影响，并且讲训练 decompose 到 Positive and Negative Sample Reinforcement (PSR and NSR) 发现如果是在负样本上进行训练能够提升模型Pass@k性能，尤其是k增大的情况下，能够和PPO，GRPO持平或者是超过。

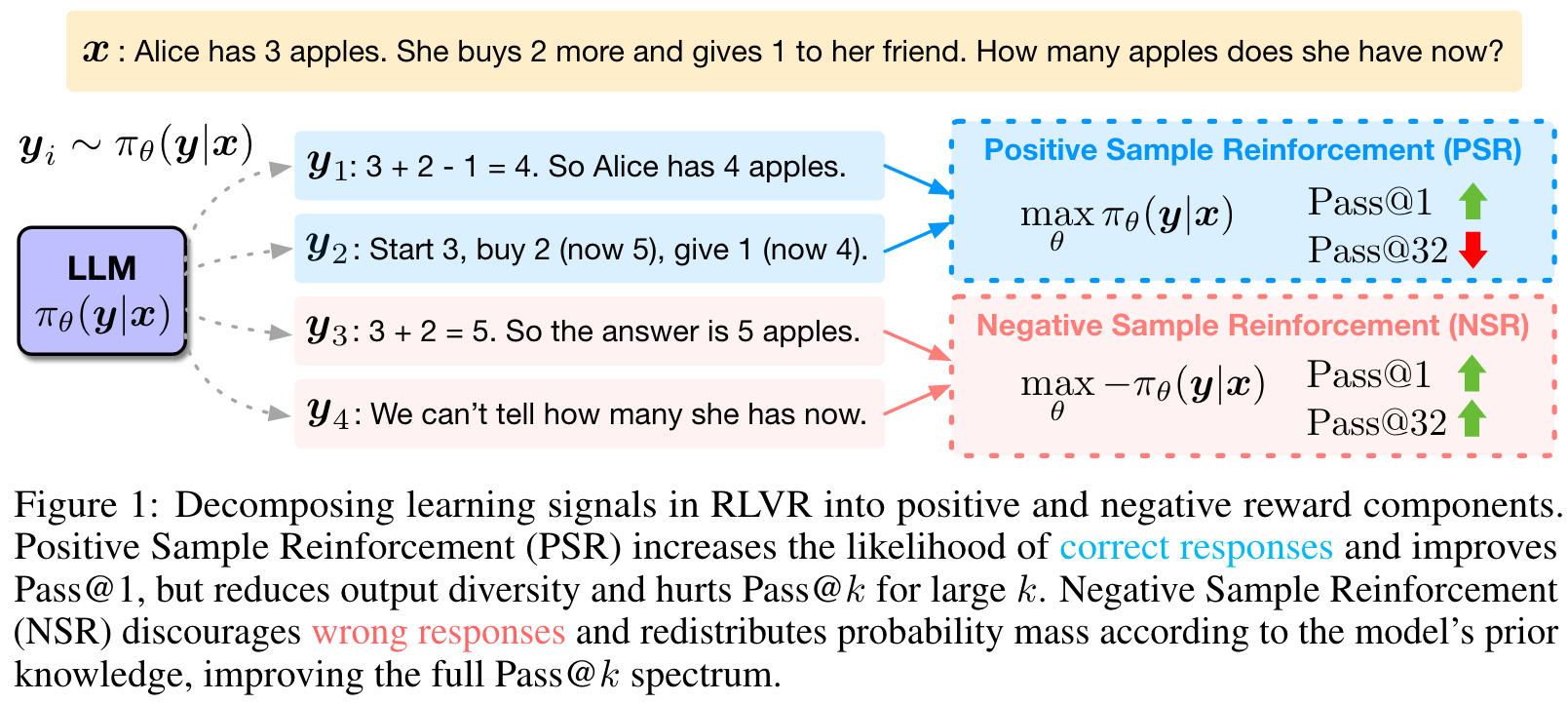
Contributions:

We decompose RLVR into two components, PSR and NSR, and investigate their distinct impacts on model behavior and generalization measured by a range of $\mathrm{Pass}@k$ metrics.
We empirically demonstrate the surprising effectiveness of NSR-only training and use gradient analysis to show that NSR refines the model's prior by suppressing incorrect reasoning steps and preserving plausible alternatives.
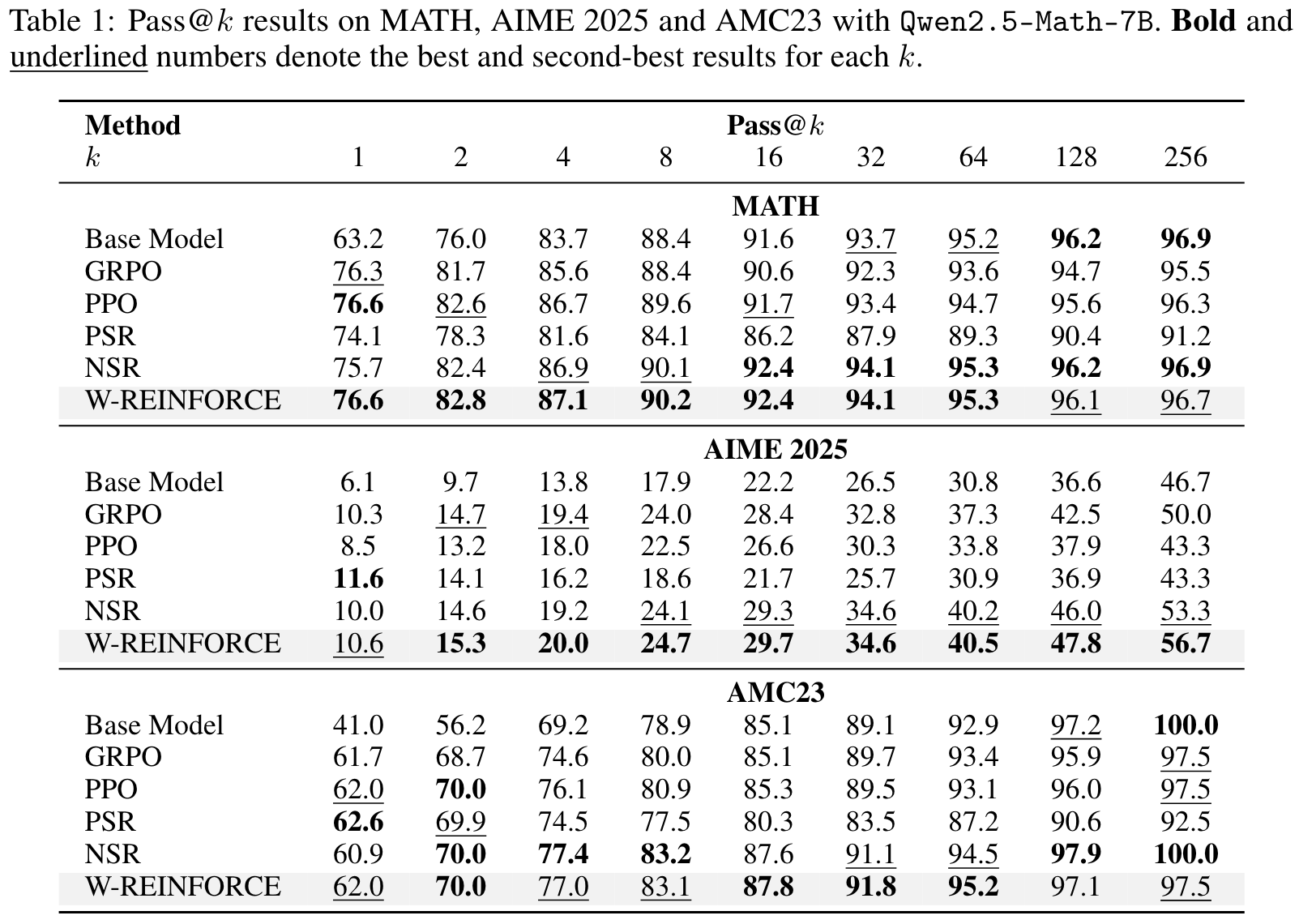
We propose Weighted-REINFORCE, a simple modification to the RL objective that upweights NSR, yielding consistent gains across complex reasoning benchmarks including MATH, AIM 2025, and AMC 23.

Main Content

The RLVR objective optimizes the expected reward-weighted likelihood:

\begin{align} \mathcal{L}_{\text{RLVR}}(\theta) &= -\mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \left[ \sum_{\boldsymbol{y}} r(\boldsymbol{x}, \boldsymbol{y}) \cdot \pi_\theta(\boldsymbol{y}|\boldsymbol{x}) \right], \quad r(\boldsymbol{x}, \boldsymbol{y}) \in \{-1, +1\} \\ &= -\mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \underbrace{\left[ \sum_{\boldsymbol{y}: r(\boldsymbol{x}, \boldsymbol{y})=1} \pi_\theta(\boldsymbol{y}|\boldsymbol{x}) \right]}_{\mathcal{L}_{\text{PSR}}(\theta)} - \mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \underbrace{\left[ \sum_{\boldsymbol{y}: r(\boldsymbol{x}, \boldsymbol{y})=-1} -\pi_\theta(\boldsymbol{y}|\boldsymbol{x}) \right]}_{\mathcal{L}_{\text{NSR}}(\theta)}, \end{align}

where we define two sub-objectives representing each learning paradigm:

\mathcal{L}_{\text{PSR}}(\theta) = -\mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \left[ \sum_{\boldsymbol{y}: r(\boldsymbol{x}, \boldsymbol{y})=1} \pi_\theta(\boldsymbol{y}|\boldsymbol{x}) \right]

\mathcal{L}_{\text{NSR}}(\theta) = -\mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \left[ \sum_{\boldsymbol{y}: r(\boldsymbol{x}, \boldsymbol{y})=-1} -\pi_\theta(\boldsymbol{y}|\boldsymbol{x}) \right].

Positive and Negative Sample Reinforcement for LLM Reasoning

Compared algorightms. We compare the performance of PSR and NSR with commonly used RL algorithms, including PPO and GRPO. PSR and NSR are implemented by selectively updating the policy model using only correct or incorrect responses, respectively. As a result, PSR and NSR are trained on fewer samples per batch than standard RL algorithms that use both correct and incorrect responses.

Training setups. For the training set, we use MATH, which contains 7,500 problems. We train the models using the verl framework. The prompt batch size is 1,024, with 8 rollouts generated per prompt. The sampling temperature during training is set to 1.0, and the maximum context length is set to 4,096 and 32,768 tokens for $\texttt{Qwen2.5-Math-7B}$ and $\texttt{Qwen3-4B}$ , respectively. We update the model with a mini-batch size of 256 and a learning rate of 1e-6.

$\mathrm{Pass}@k$ is defineed as the fraction of problems for which at least one correct response is produced in $k$ independent trials. However, directly computing $\mathrm{Pass}@k$ using only $k$ samples per example often suffers from high variance. We follow the unbiased estimator, which generates $n$ samples per problem ( $n\geq k$ ), counts the number of correct responses $c$ , and computes an unbiased estimate of $\mathrm{Pass}@k$ as:

\text{Pass}@k = \mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \left[ 1 - \frac{\binom{n-c}{k}}{\binom{n}{k}} \right]

Notably, varying $k$ provides insights into different aspects of model behaviors. $\mathrm{Pass}@1$ approximates greedy decoding accuracy, reflecting how confidently the model can produce a correct response in a single attempt, essentially reflecting exploitation. In contrast, $\mathrm{Pass}@k$ with large $k$ evaluates the model's ability to generate diverse correct responses across multiple attempts, capturing its exploration ability and reasoning boundary.

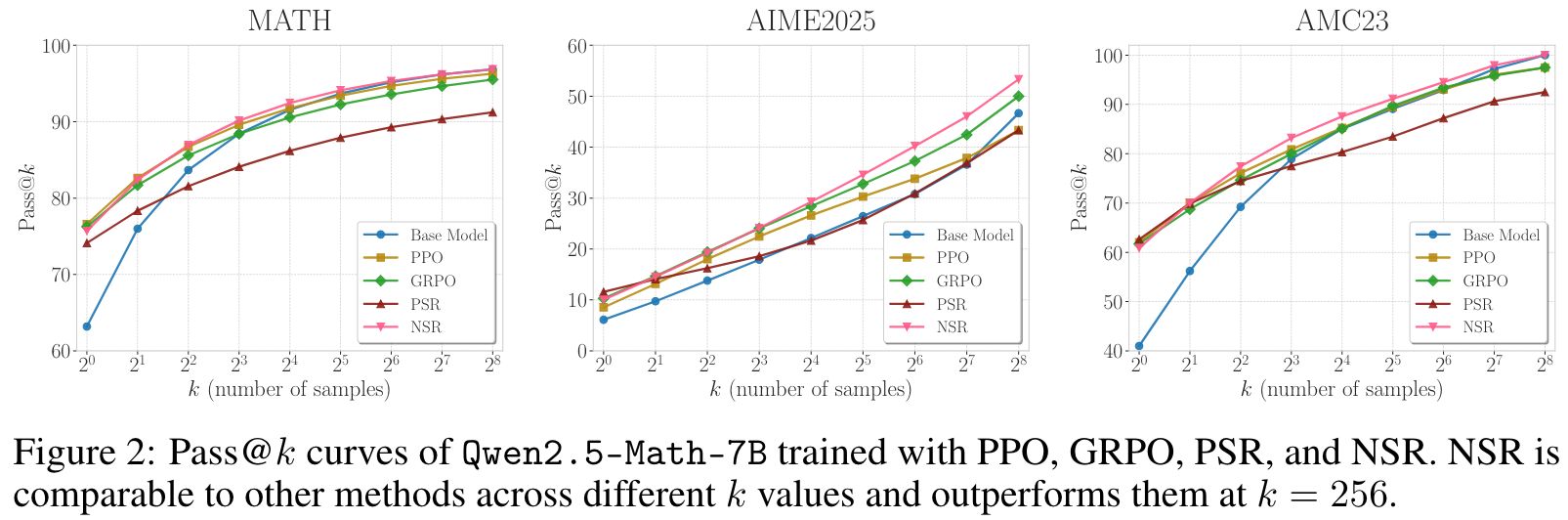
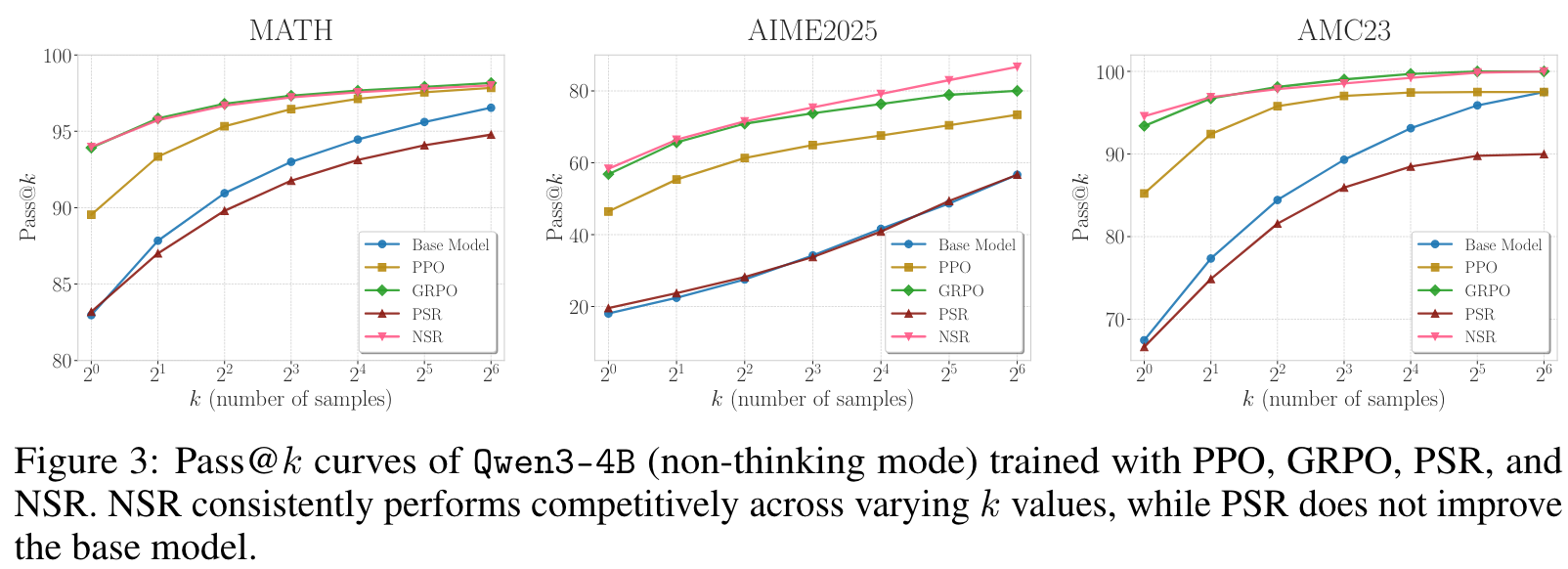
NSR outperforms or stays comparable to the base model at a large $k$ value. At larger decoding budgets (e.g., $\mathrm{Pass}@256$ ), recent work shows that RL-trained models often lose their advantage, and in some cases underperform the base model. This trend is generally observed in our experiments with PPO, GRPO, and PSR, especially in Figure 2.

PSR improves accuracy at the cost of diversity. This behaviors indicates that PSR overly concentrates probability mass on early correct responses, leading to overconfidence and a collapsed output distribution and ultimately limiting the model's ability to generate deiverse correct responses when allowing for more test-time compute.

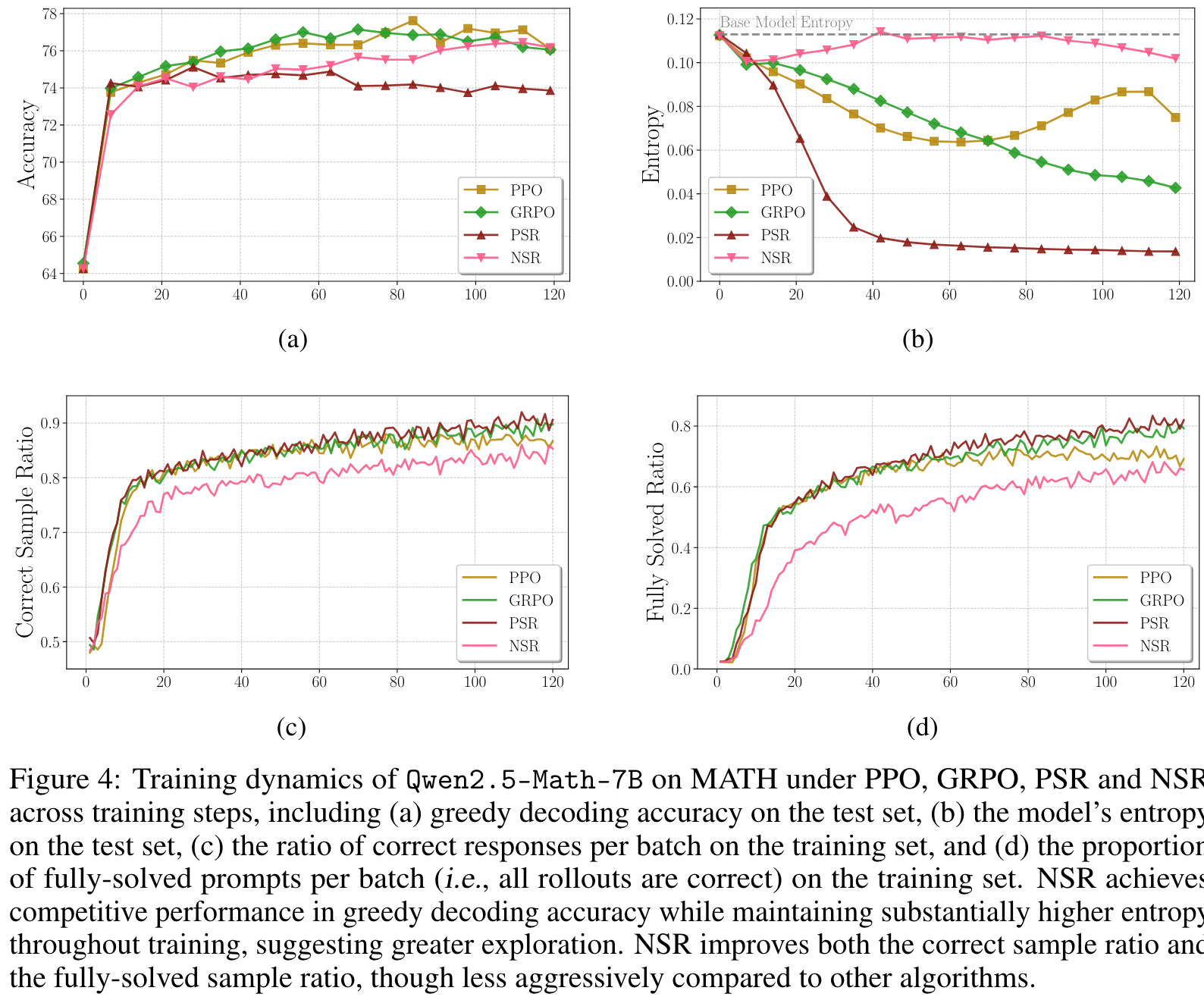
Token-Level Gradient Dynamics of PSR and NSR

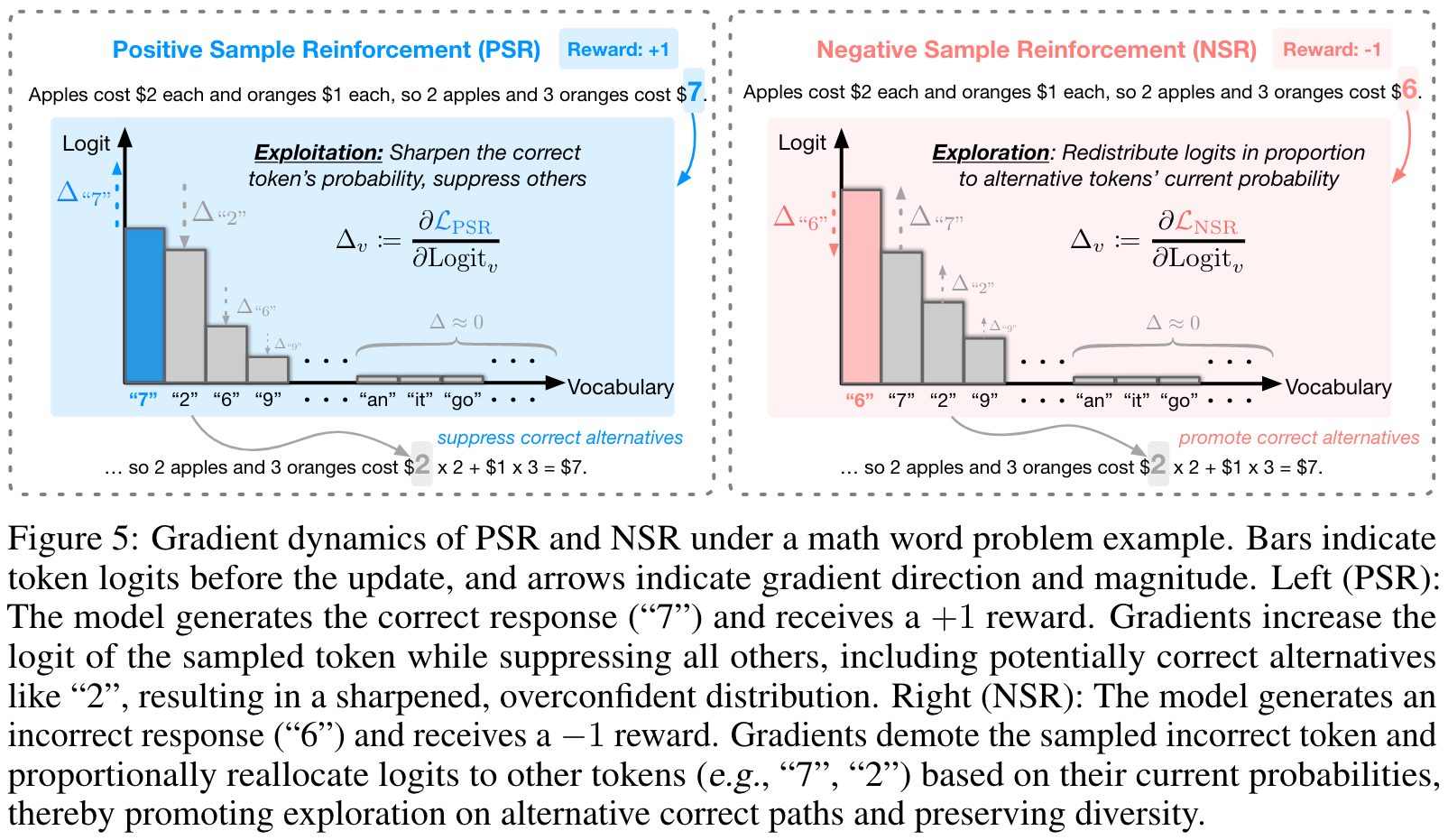
Balancing Positive and Negative Reinforcement

🤖

论文的创新之处与独特性：
- 创新点1：负样本强化(NSR)的提出及其有效性分析
  论文通过将强化学习中的奖励机制分解为正样本强化(PSR)和负样本强化(NSR)，揭示了负样本强化在提升语言模型推理能力中的重要作用。尤其是单独使用负样本强化可以显著提高模型在推理任务中的表现，同时保持生成的多样性，甚至在某些情况下超过了主流的强化学习算法（如PPO和GRPO）。这一发现挑战了传统观点，即正样本奖励是提升模型性能的主要驱动力。
- 创新点2：梯度分析揭示负样本强化的机制
  通过梯度分析，论文详细阐述了NSR如何通过抑制错误生成并重新分配概率质量来优化模型的输出。这种方法有效地利用了模型的先验知识，同时避免了过拟合和生成多样性下降的问题。
- 创新点3：提出Weighted-REINFORCE算法
  论文提出了一种简单但有效的加权强化学习算法（Weighted-REINFORCE），通过降低正样本奖励的权重来平衡PSR和NSR的优势，最终在多个推理基准上表现出色。这一算法为设计高效的强化学习目标函数提供了新的思路。
- 关键学习点
  - NSR能够在不直接强化正确样本的情况下间接提高模型的推理能力。
  - 正样本奖励可能导致输出分布的过度集中，损害模型的生成多样性。
  - 通过调整奖励权重，可以实现准确性和多样性之间的平衡。
论文中存在的问题及改进建议：
- 问题1：对更广泛模型的适用性验证不足
  论文的实验主要集中在Qwen2.5-Math-7B和Qwen3-4B模型上，这些模型在数学推理任务中表现优异。然而，不同模型的先验知识和推理能力可能差异显著，NSR和Weighted-REINFORCE的适用性尚未在其他模型（如GPT系列或其他开源模型）上得到验证。
  - 改进建议：扩展实验范围，选择不同架构和规模的模型进行验证，以评估NSR和Weighted-REINFORCE的通用性。
- 问题2：长期训练稳定性问题
  论文提到，长时间使用NSR训练可能导致模型性能下降，表明NSR在稳定性方面存在一定局限性。
  - 改进建议：研究动态调整NSR和PSR权重的方法，例如在训练初期使用更多的NSR，后期逐步增加PSR的权重，以确保训练的稳定性。
- 问题3：对复杂奖励信号的适应性研究不足
  论文主要研究了二元奖励信号(+1/-1)的情况，而实际任务中可能存在更复杂的奖励信号（例如连续值或多维反馈）。
  - 改进建议：探索NSR和Weighted-REINFORCE在复杂奖励信号下的表现，并设计新的目标函数以适应这些场景。
基于论文的内容和研究结果，提出的创新点或研究路径：
- 创新点1：动态权重调整的强化学习方法
  设计一种动态权重调整机制，根据模型的训练阶段或任务类型动态调整PSR和NSR的权重，以优化训练效果。
- 创新点2：跨领域任务上的NSR应用研究
  将NSR应用于其他推理任务（如代码生成、科学问题解答或开放领域问答），验证其在不同任务中的适用性和效果。
- 创新点3：复杂奖励信号下的强化学习目标函数设计
  针对复杂奖励信号（例如连续值或多维反馈），设计新的强化学习目标函数，将NSR的概率分布重分配特性与奖励信号的细粒度信息结合。
为新的研究路径制定的研究方案：
- 研究路径1：动态权重调整的强化学习方法
  - 研究方法：设计一种动态权重调整机制，在训练过程中根据模型的准确性和生成多样性动态调整PSR和NSR的权重。可以通过监控模型的预测熵和正确样本比例来决定权重变化。
  - 研究步骤：
    1. 实现动态权重调整算法，并与固定权重的Weighted-REINFORCE进行对比。
    2. 在数学推理任务上进行实验，评估动态权重调整的效果。
    3. 分析权重变化对模型性能的影响，验证其是否能够改善训练稳定性。
  - 期望成果：动态权重调整能够在训练过程中平衡准确性和多样性，提升模型性能，同时保持训练稳定性。
- 研究路径2：跨领域任务上的NSR应用研究
  - 研究方法：将NSR应用于不同领域的推理任务（如代码生成、科学问题解答），并与主流强化学习算法（如PPO、GRPO）进行对比。
  - 研究步骤：
    1. 选择多个跨领域任务数据集（如CodeXGLUE、SciQ等）。
    2. 在不同任务上单独训练NSR，并与PSR、PPO等方法进行性能比较。
    3. 分析任务特性对NSR效果的影响，探索其适用范围。
  - 期望成果：验证NSR在不同任务中的通用性，并发现其在特定任务上的潜在优势。
- 研究路径3：复杂奖励信号下的强化学习目标函数设计
  - 研究方法：设计新的目标函数，将NSR的概率分布重分配特性与复杂奖励信号结合，例如通过加权平均或正则化方式处理多维奖励信号。
  - 研究步骤：
    1. 定义复杂奖励信号的形式（如连续值或多维反馈）。
    2. 设计新的目标函数，并实现相应的训练算法。
    3. 在包含复杂奖励信号的任务数据集上进行实验，评估新目标函数的效果。
    4. 与传统强化学习算法进行对比，分析其在复杂奖励场景中的优势。
  - 期望成果：新的目标函数能够有效处理复杂奖励信号，同时保持NSR的优势，提升模型在实际任务中的表现。

目录

Summary Overview

Main Content

🤖

Others