Resource Info
Paper http://arxiv.org/abs/2505.18116
Code & Data https://github.com/NVlabs/NFT
Public arXiv
Date 2025.08.13

Resource	Info
Paper	http://arxiv.org/abs/2505.18116
Code & Data	https://github.com/NVlabs/NFT
Public	arXiv
Date	2025.08.13

Summary Overview

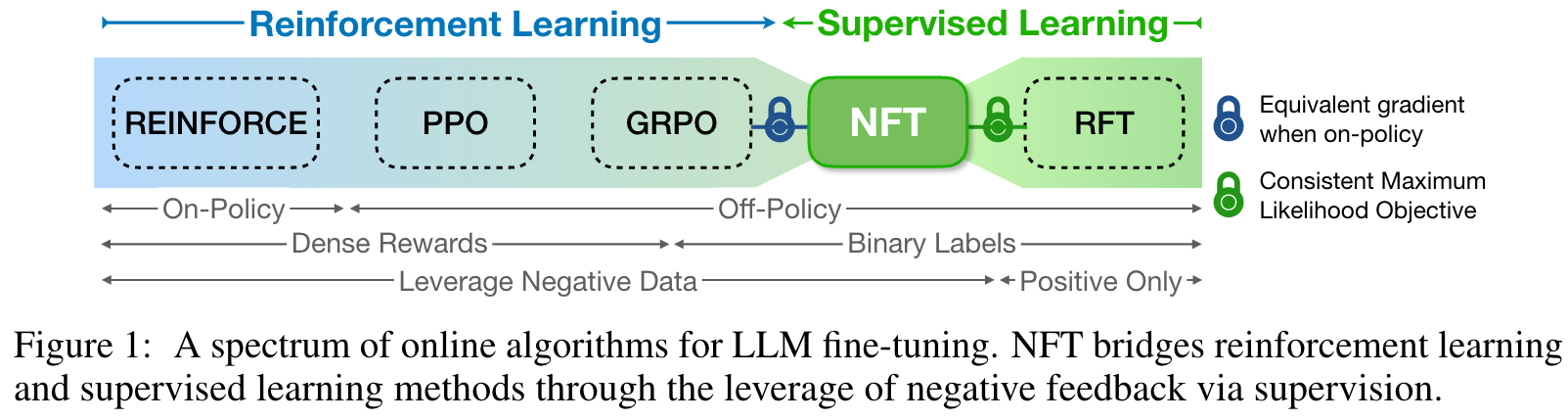
NFT 提出了一种监督学习的方法，与普通的 SFT 不同的是，NFT能够和 RL 一样从错误中学习。传统的监督学习中，RFT 只使用了正确的答案进行训练，而 NFT 则是能够将模型生成的错误答案利用起来。同时作者也证明了，在 on-policy 训练中，NFT 和 GRPO 这样的 RL 算法是等价的。

Main Content

Rejection sampling Fine-Tuning (RFT): At each iteration, an LLM generates answers to questions. A verifier helps reject all negative answers. The remaining positive ones are compiled into a dataset to fine-tune the LLM itself in a supervised manner.

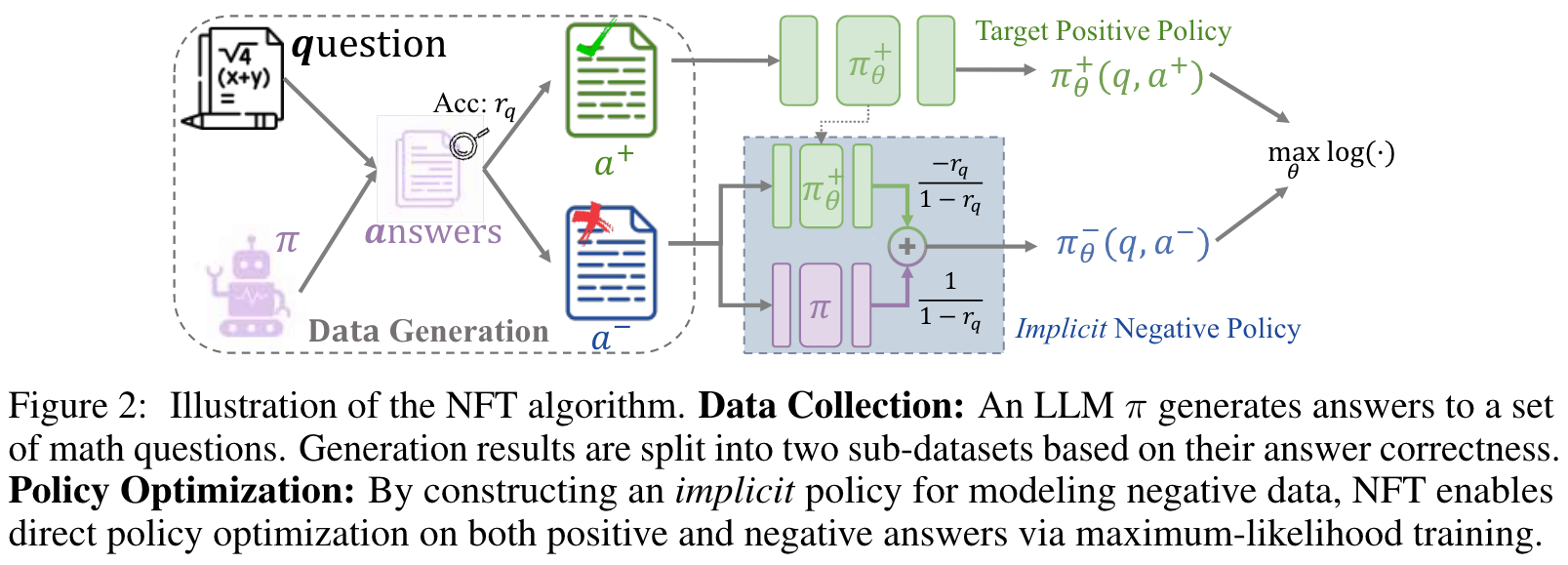
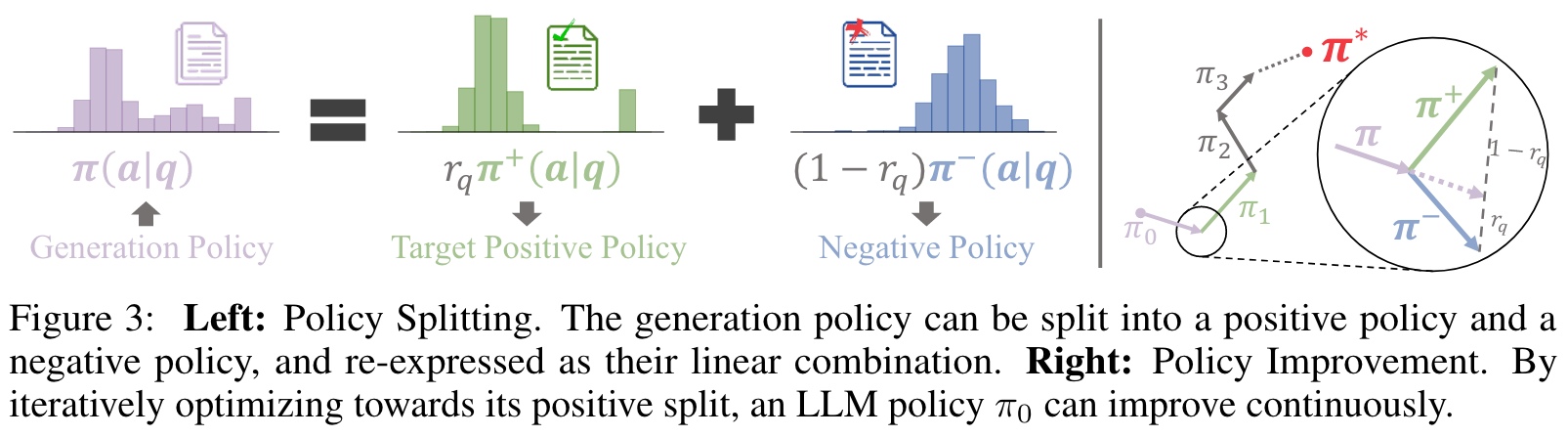
NFT (Negative-aware Fine-Tuning) 算法的核心思想是，通过构建一个隐式负策略来使得 LLM 自己能够从错误的答案中进行训练，从而弥补传统监督学习在利用负反馈方面的不足。

首先，给定一组数学问题 $q$ 和一个预训练的LLM $\pi(a|q)$ ，以及一个用于验证答案正确性的炎症期，在每次迭代中，模型会生成一组答案 $a^{1:K}$ ，并根据 verifier 得到它们的正确性标签 $r^{1:K}\in\{0,1\}$ 。这些数据被分为两部分：正确的答案集 $\mathcal{D}^+$ 和 $\mathcal{D}^-$ 。接着，作者定义了两种策略:

Target Positive Policy $\pi^+(a|q)$ : 这是模型希望学习的策略，即在给定问题 $q$ 的情况下，生成正确答案 $a$ 的条件概率。根据贝叶斯定理，这个策略可以表示为:

\pi^+(a|q):=\pi(a|q,r=1)=\frac{\pi(a|q)p(r=1|q,a)}{\sum_A\pi(a|q)p(r=1|q,a)}

Implicit Negative Policy $\pi^-(a|q)$ : 这是生成错误答案的策略，同样可以由贝叶斯定理表示:

\pi^-(a|q):=\pi(a|q,r=0)=\frac{\pi(a|q)[1-p(r=1|q,a)]}{\sum_A\pi(a|q)[1-p(r=1|q,a)]}

将 $\pi^-(a|q)$ 用目标正策略 $\pi^+(a|q)$ 和原始策略 $\pi(a|q)$ 来重新参数化。这个被重新参数化的负策略就是所谓的隐式负策略 $\pi^-_\theta$ 。

\pi_\theta^-(a|q):=\frac{\pi(a|q)-r_q\pi_\theta^+(a|q)}{1-r_q}

这样一来，在负样本上进行的任何训练，都会直接优化底层的正向策略 $\pi_\theta^+$ 。

最后的 Loss 函数结合正向数据和负向数据的优化。这个损失函数是通过最大似然目标来推导的。

对正向数据的损失：其目标是最大化正确的答案似然 $\log(\pi_\theta^+(a|q))$
对负向数据的损失：其目标是最大化隐式策略的似然 $\log(\pi_\theta^-(a|q))$

将这两部分结合起来，得到 Loss

\mathcal{L}_{(a,q,r)\sim\mathcal{D}}^{\text{NFT}}(\theta) = r\left[-\log\frac{\pi_\theta^+(a|q)}{\pi(a|q)}\right] + (1-r)\left[-\log\frac{1-r_q\frac{\pi_\theta^+(a|q)}{\pi(a|q)}}{1-r_q}\right]

加上一些实践上的改进，NFT 得到了最终的 Loss 函数 (+ Token-level loss + Clipping negative likelihood ratio + Prompt weighting)。

\mathcal{L}_{\mathcal{D}}^{\text{NFT}}(\theta) = -\sum_{q,a,r} \omega(q) \sum_t \left[ r \log R_\theta^t(q,a) + (1-r) \log \text{max\_v}\left(\frac{1-\hat{r}_q R_\theta^t(q,a)}{1-\hat{r}_q}, \epsilon\right) \right]

where $R_\theta^t(q,a) = \frac{\pi_\theta^+(a_t|q,a_{<t})}{\pi(a_t|q,a_{<t})}$ , and $\hat{r}_q = \frac{1}{K}\sum_{a|q} r(q,a)$

Experiments

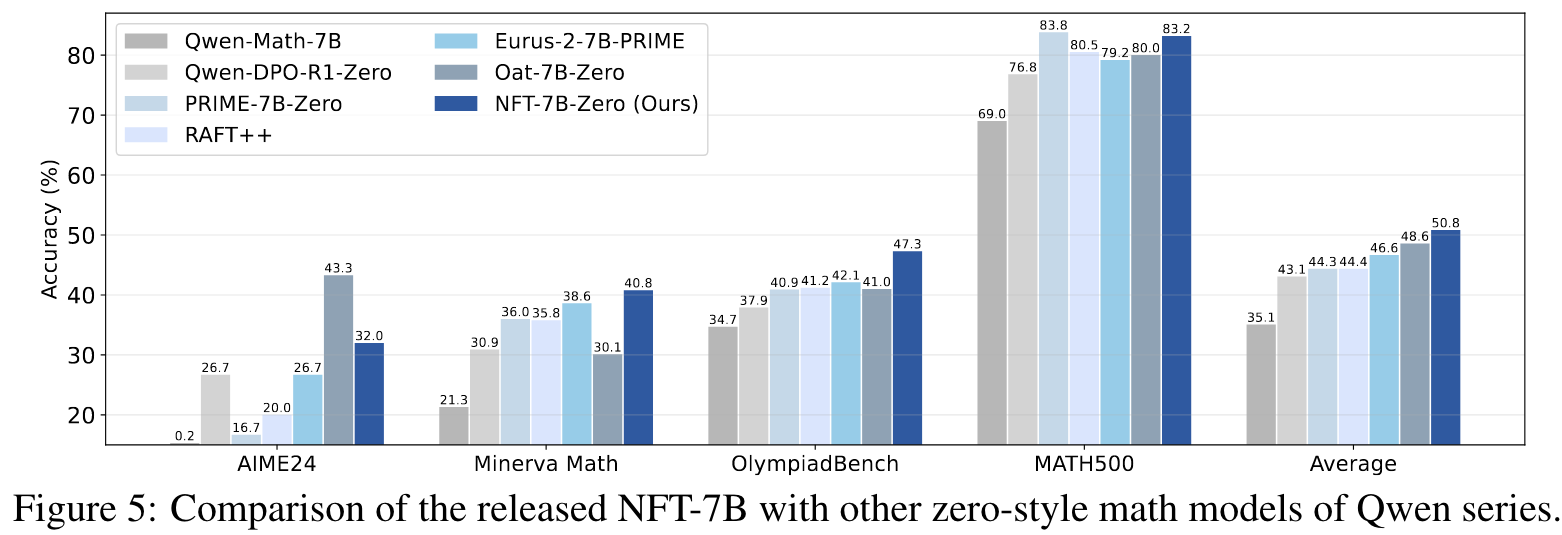
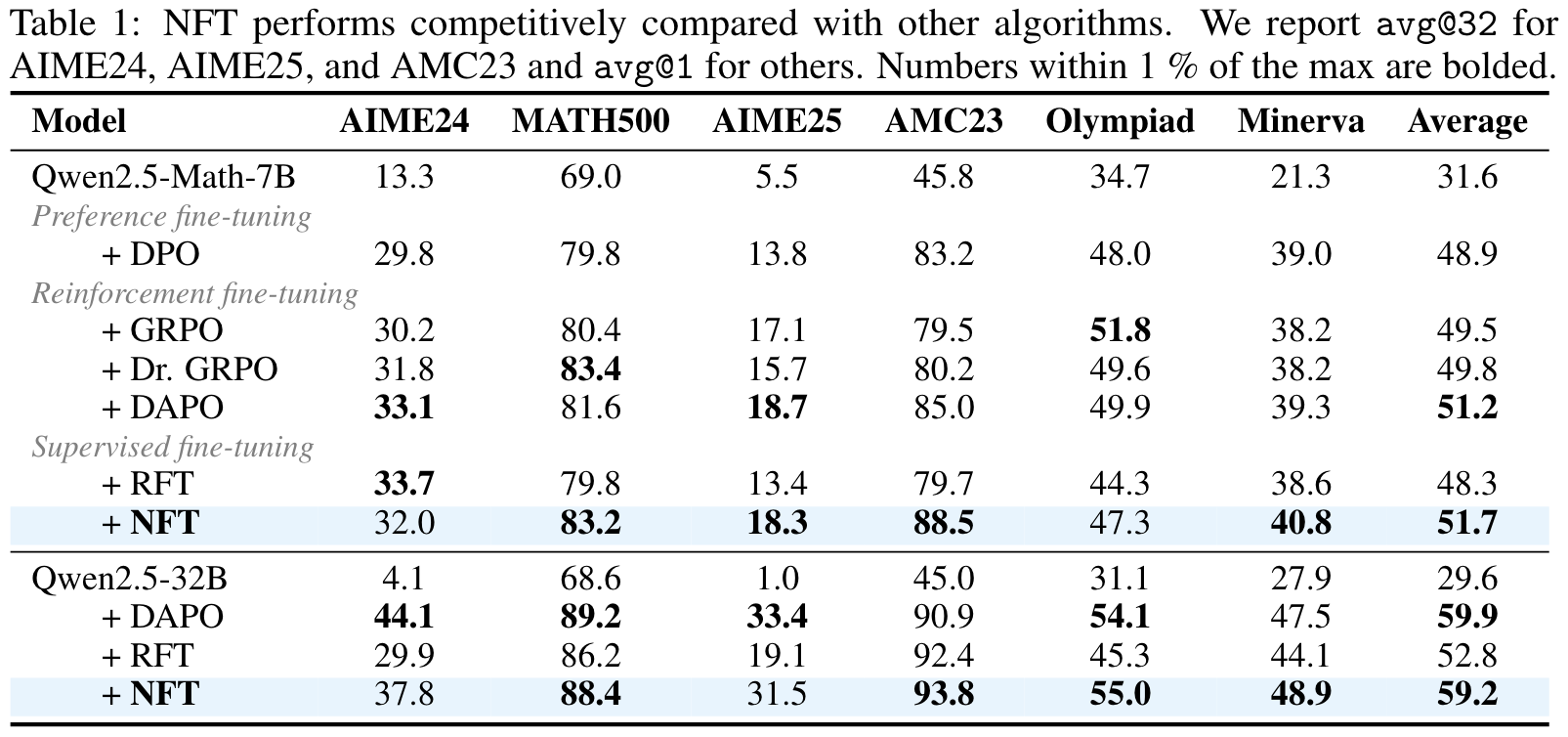
Benefits of Negative Data

🤖

论文的创新之处与独特性：
- 提出NFT算法，桥接SL与RL的理论与实践：论文提出了“Negative-aware Fine-Tuning (NFT)”算法，这是一种基于监督学习（SL）的新方法，能够通过负反馈数据实现自我改进。相比传统SL仅使用正样本，NFT引入了隐式负策略，通过最大似然优化同时学习正负样本。这种方法不仅显著提升了LLMs的数学推理能力，还在严格的on-policy条件下与领先的RL算法（如GRPO）表现出理论等价性。
- 挑战传统观点，拓展SL的应用边界：传统观点认为SL无法通过负反馈实现自我改进，而论文通过理论分析和实验验证表明，SL在使用负反馈数据时可以达到甚至超越RL的效果。这一发现为SL在二元反馈系统中的应用开辟了新的可能性。
- 极简设计与高效实现：NFT算法仅需维护一个模型，避免了复杂的多模型架构，减少了内存开销，同时通过负样本的隐式建模实现了直接优化。这种设计在训练效率和资源节约方面具有显著优势。
- 实验验证与广泛比较：论文在7B和32B规模的模型上进行了广泛实验，结果显示NFT在数学推理任务中表现优异，甚至与领先的RL算法（如DAPO）持平或超越。这证明了NFT的稳定性和有效性。
论文中存在的问题及改进建议：
- 负反馈数据的利用效率问题：虽然NFT引入了负反馈数据，但论文中未深入探讨如何进一步挖掘负样本的潜在价值。例如，负样本可能包含某些模式或错误类型，这些信息可以用于更细粒度的优化策略设计。建议引入负样本分类机制，根据错误类型调整模型的学习权重。
- 缺乏对模型泛化能力的深入分析：论文主要关注数学推理任务，但未明确讨论NFT在其他领域（如语言生成、逻辑推理等）的泛化能力。建议扩展实验范围，验证NFT在更多任务中的适用性，并分析其潜在局限性。
- 算法对超参数敏感性问题：论文中提到负比率剪裁参数（[\epsilon]）对模型性能影响较大，但未提供详细的超参数调优方法。建议进行系统的超参数敏感性分析，并提出自动调优策略以提升算法的鲁棒性。
- 对RL与SL理论等价性的进一步扩展：虽然论文证明了NFT与GRPO在on-policy条件下的等价性，但未探讨off-policy条件下的差异及潜在改进方向。建议研究如何在off-policy条件下缩小SL与RL的性能差距。
基于论文的内容和研究结果，提出的创新点或研究路径：
- 研究路径1：基于负样本分类的动态优化策略
  通过对负样本进行错误类型分类（如计算错误、逻辑错误、表达错误等），设计动态优化策略，使模型针对不同类型的错误进行有针对性的学习。
- 研究路径2：跨任务泛化能力的验证与改进
  将NFT应用于其他领域（如语言生成、代码推理等），验证其泛化能力，并探索如何通过任务迁移学习进一步提升模型性能。
- 研究路径3：结合RL与SL的混合优化框架
  在NFT的基础上引入RL奖励信号，设计混合优化框架，综合利用SL的效率和RL的探索能力，进一步提升模型的自我改进能力。
为新的研究路径制定的研究方案：
- 研究路径1：基于负样本分类的动态优化策略
  - 研究方法：通过分析负样本的错误类型，构建分类器对负样本进行分类；根据分类结果设计动态权重调整机制，使模型在训练过程中对不同类型的错误给予不同的关注。
  - 研究步骤：
    1. 收集负样本数据并进行错误类型标注。
    2. 训练分类器对负样本进行自动分类。
    3. 根据分类结果调整NFT的优化目标，设计动态权重调整机制。
    4. 在数学推理任务上验证动态优化策略的效果。
  - 期望成果：显著提升模型对负样本的学习效率，降低错误率，同时提高模型的数学推理能力和稳定性。
- 研究路径2：跨任务泛化能力的验证与改进
  - 研究方法：将NFT应用于不同任务（如语言生成、代码推理等），并引入迁移学习方法以提升跨任务性能。
  - 研究步骤：
    1. 选择多个任务，构建对应的训练数据集。
    2. 将NFT应用于每个任务，记录模型性能。
    3. 引入迁移学习方法（如多任务学习或知识蒸馏），探索跨任务性能提升的可能性。
    4. 分析NFT在不同任务中的局限性，并提出改进建议。
  - 期望成果：验证NFT的跨任务泛化能力，提出适用于多任务的优化方法，为SL在更多领域的应用提供理论与实践支持。
- 研究路径3：结合RL与SL的混合优化框架
  - 研究方法：设计混合优化框架，将RL奖励信号与NFT的负样本优化目标结合，综合利用两者的优势。
  - 研究步骤：
    1. 在NFT的基础上引入RL奖励信号，设计混合优化目标。
    2. 通过实验验证混合优化框架的性能，并与单一算法（如NFT或GRPO）进行对比。
    3. 分析混合优化框架的适用场景及潜在问题。
    4. 优化框架设计，提升其鲁棒性和适用性。
  - 期望成果：提出一种性能更优的混合优化框架，在数学推理任务及其他领域实现显著性能提升，同时拓展SL与RL结合的理论边界。

目录

Summary Overview

Main Content

Experiments

🤖

Others